Nếu bạn muốn biết cách tính diện tích toàn phần hình trụ để giải bài tập, hãy tham khảo ngay công thức và phương pháp tính diện tích toàn phần hình trụ dưới đây.
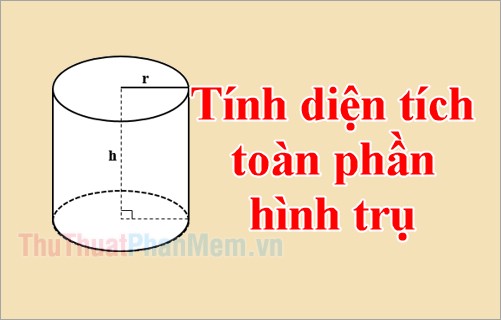
Hình trụ tròn là một hình trụ có hai đáy là hai đường tròn bằng nhau. Diện tích toàn phần của hình trụ bằng diện tích xung quanh cộng với diện tích của cả hai đáy.
Cho hình trụ có chiều cao là h và bán kính đáy là r, ta có thể sử dụng công thức như hình vẽ.
Diện tích xung quanh hình trụ
Sxq=2πrhSxq=2πrh
Diện tích 2 đường tròn đáy
S2đ=2πr2(Sđ=πr<span>2)S2đ=2πr2(Sđ=πr2)
=> Diện tích toàn phần hình trụ:
Stp=2πr2+2πrh=2πr(r+h)Stp=2πr2+2πrh=2πr(r+h)
Trong đó:
- SxqSxq là diện tích xung quanh hình trụ.
- S2đS2đ là diện tích 2 đường tròn đáy hình trụ, Sđ là diện tích đường tròn đáy.
- StpStp là diện tích toàn phần hình trụ.
- ππ là hằng số ππ = 3.14159265359
- r là bán kính đường tròn đáy.
- h là chiều cao hình trụ.
Bí quyết tính diện tích toàn phần hình trụ
Để có diện tích toàn phần hình trụ, bạn chỉ cần tính tổng diện tích đáy và diện tích xung quanh sau đó cộng lại:
1. Đầu tiên, tính diện tích đáy hình trụ bằng cách sử dụng công thức Sđ Sđ
Sđ=πr2Sđ=πr2
Nếu bạn có bán kính r, áp dụng công thức ngay. Nếu chưa biết r, hãy tìm r từ dữ liệu và sau đó tính diện tích đáy hình trụ.
2. Tiếp theo, tính diện tích xung quanh hình trụ
Công thức diện tích xung quanh hình trụ Sxq=2πrhSxq=2πrh
Chiều cao thường được cung cấp, bán kính r đã có từ bước 1, giờ bạn chỉ cần tính diện tích xung quanh hình trụ.
3. Cuối cùng, áp dụng công thức tính diện tích toàn phần hình trụ
Stp=2.Sđ+SxqStp=2.Sđ+Sxq
Hoặc bạn có thể tìm bán kính r và chiều cao h từ yêu cầu của đề bài, sau đó áp dụng công thức tính diện tích toàn phần hình trụ:
Stp=2πr2+2πrh=2πr(r+h)Stp=2πr2+2πrh=2πr(r+h)
Một ví dụ
Ví dụ 1: Tính diện tích toàn phần của hình trụ, đường kính đáy là 10cm, và chiều cao là 6cm.
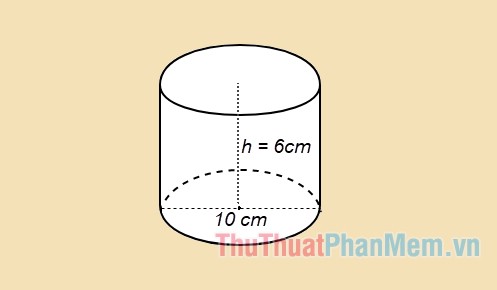
Giải
Theo đề bài, có: h = 6cm; đường kính đáy 2r = 10cm => r = 5cm.
Áp dụng công thức tính diện tích toàn phần hình trụ:
Stp=2πr(r+h)=2π.5(5+6)=110π(cm2)Stp=2πr(r+h)=2π.5(5+6)=110π(cm2)
=> Vậy diện tích toàn phần của hình trụ là 110π(cm2)110π(cm2)
Ví dụ 2: Tính diện tích toàn phần của hình trụ với chiều cao 7cm và diện tích xung quanh là 310 (cm2)(cm2)
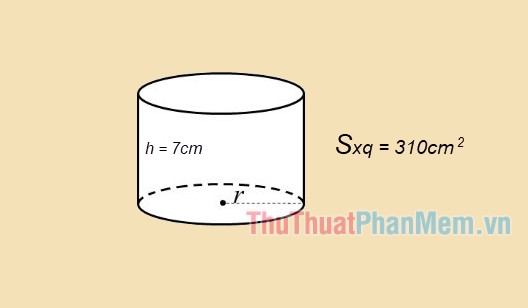
Giải
Theo đề bài, có h = 7; Sxq=310Sxq=310
Áp dụng công thức tính diện tích xung quanh Sxq=2πrhSxq=2πrh
=> r=Sxq2πrh=3102π.7≈7cmr=Sxq2πrh=3102π.7≈7cm
Vậy SĐ=πr2=π.72=49π≈154cm2SĐ=πr2=π.72=49π≈154cm2
=> Diện tích toàn phần của hình trụ: Stp=2.Sđ+Sxq=2.154+310=618cm2Stp=2.SĐ+Sxq=2.154+310=618cm2
Trên đây bài viết đã chia sẻ đến các bạn công thức, ví dụ cụ thể về cách tính diện tích toàn phần hình trụ. Hi vọng bài viết sẽ giúp các bạn hiểu rõ hơn về cách tính diện tích toàn phần hình trụ để áp dụng tính toán cho các bài toán cụ thể. Chúc các bạn thành công!