Định lí Pythagore và ứng dụng| Toán 8 chương trình mới

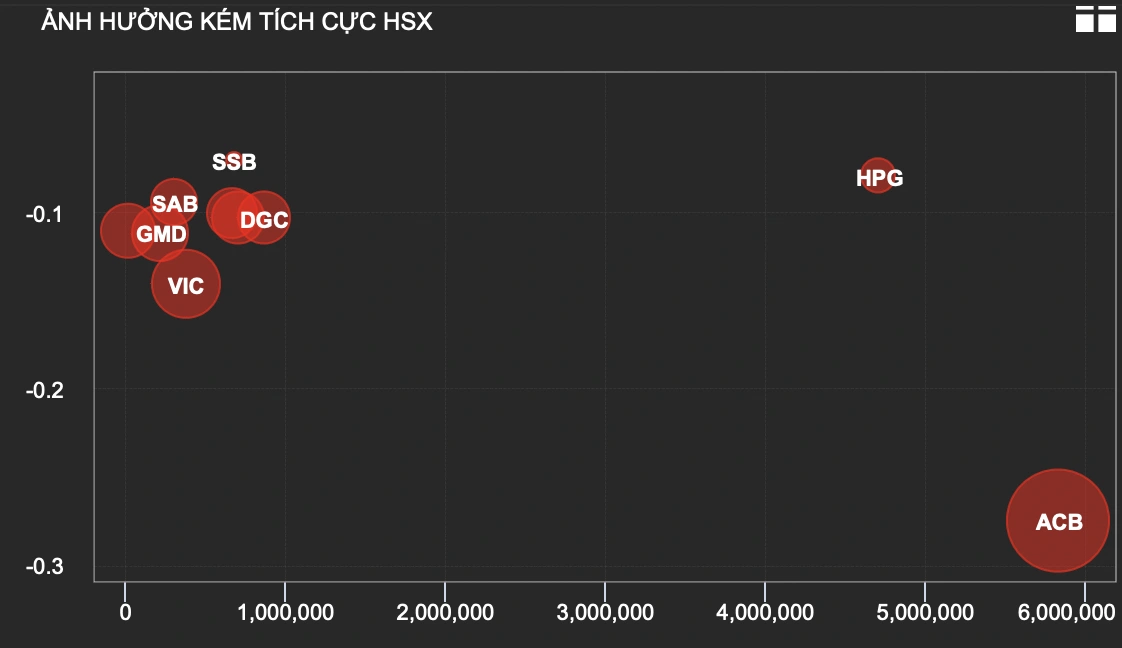
1. Định lý pythagore toán 8

- Trong một tam giác vuông, bình phương của cạnh huyền bằng tổng các bình phương của hai cạnh góc vuông.

- Chứng minh định lý:

Giả thiết: $\large \Delta ABC; \widehat{A}=90^{o}$

Kết luận: BC2 = AB2 + AC2

Chứng minh:

Kẻ đường cao AH của tam giác ABC.

Hai tam giác ABC và HBA có: $\large \widehat{BAC}=90^{o}=\widehat{BHA}; \widehat{B}$ chung.

Vậy $\large \Delta ABC \sim \Delta HBA(g.g)$

$\large \Rightarrow \frac{AB}{HB}=\frac{BC}{AB}$ hay $\large AB^{2}=HB.BC$ (1)

Tương tự, $\large \Delta ABC \sim \Delta HAC(g.g)$

$\large \Rightarrow \frac{AC}{HC}=\frac{BC}{AC}$ hay $\large AC^{2}=HC.BC$ (2)

Từ (1) và (2) => AB2 + AC2 = (HB + HC).BC = BC2

2. Định lý pythagore đảo toán 8

- Nếu một tam giác có bình phương độ dài của một cạnh bằng tổng cách bình phương độ dài của hai cạnh kia thì tam giác đó là tam giác vuông.

3. Ứng dụng của định lý pythagore toán 8

3.1 Tính độ dài đoạn thẳng

Bài toán: Cho tam giác ABC vuông tại A, có AB = 6cm, AC = 8cm. Hãy tính độ dài cạnh BC, đường cao AH và các đoạn thẳng BH, CH.

Lời giải:

Áp dụng định lý pythagore cho tam giác vuông ABC, ta được:

BC2 = AB2 + AC2 = 62 + 82 = 100 hay BC = 10cm.

Vì diện tích của tam giác ABC bằng $\large \frac{AB.AC}{2}=\frac{AH.BC}{2}$

$\large \Rightarrow AH=\frac{AB.AC}{BC}=\frac{6.8}{10}=4,8cm$

Áp dụng định lý pythagore cho tam giác vuông AHB, ta được:

BH2 = AB2 - AH2 = 62 - 4,82 = 12,96 => BH = 3,6cm.

=> CH = BC - BH = 10 - 3,6 = 6,4cm

Nhận xét: Nếu tam giác vuông ABC cân tại A có đường cao AH = h, các cạnh BC = a, AC = b, AB = c thì h.a = b.c

3.2 Chứng minh tính chất hình học

Bài toán: Một chiếc cột có chiều cao h dựng thẳng đứng trên mặt đất tại điểm M, người ta kéo căng các sợi dây từ đỉnh cột (điểm A) lần lượt đến các điểm C và D trên mặt đất. Biết rằng CM = c; DM = d và c < d. Hãy chứng minh rằng a < b. Lời giải:

Áp dụng định lý pythagore cho hai tam giác vuông AMC và AMD, ta được:

AC2 = AM2 + CM2, hay a2 = h2 + c2 (1)

và AD2 = AM2 + DM2, hay b2 = h2 + d2 (2)

Vì c < d nên từ (1) và (2) => a2 < b2. Do đó a < b.

Lộ trình khóa học DUO sẽ được thiết kế riêng cho từng nhóm học sinh, phù hợp với khả năng của các em cũng như giúp các em từng bước đạt điểm 9, 10 trong mọi bài kiểm tra.

Định lí Pythagore và ứng dụng| Toán 8 chương trình mới

4. Bài tập về định lý pythagore toán 8

4.1 Bài tập về định lý pythagore toán 8 kết nối tri thức

Bài 9.17

Tam giác ABC vuông tại A thì BC là cạnh huyền.

Khi đó, theo định lí Pythagore, ta có BC2 = AB2 + AC2 => BC2 - AC2 = AB2 hay BC2 − AB2 = AC2.

Do đó b) và d) là khẳng định đúng; a) và c) là khẳng định sai.

Bài 9.18

Do 1 + 1 = 2 và 2 + 4 = 6 < 20 nên các bộ ba trong a) , b) đều không thỏa mãn bất đẳng thức tam giác nên không thể là độ dài ba cạnh của một tam giác.

Vì 52 = 32 + 42 và $\large (2\sqrt{2})^{2}=2^{2}+2^{2}$ nên các bộ ba trong c), d) là độ dài ba cạnh của tam giác vuông (theo định lí Pythagore đảo).

Bài 9.19

Các tam giác trong hình đều là các tam giác vuông nên ta áp dụng định lí Pythagore.

+) x2 = 42 + 22 = 20. Suy ra x = $\large 2\sqrt{5}$ .

+) 52 = 42 + y2 nên y2 = 52 − 42 = 9. Suy ra y = 3.

+) z2 = $\large (\sqrt{5})^{2}+(2\sqrt{5})^{2}$ = 25. Suy ra z = 5.

+) t2 = 12 + 22 = 5. Suy ra t = $\large \sqrt{5}$ .

Bài 9.20

Vì tam giác ABC cân tại A có đường cao AH nên AH cũng là đường trung tuyến hay H là trung điểm BC. Suy ra HB = HC = BC : 2 = 10 : 2 = 5 cm.

Xét tam giác AHB vuông tại H, theo định lí Pythagore ta có

AB2 = AH2 + HB2 = 32 + 52 = 34.

Suy ra AB = $\large \sqrt{34}$ cm.

Do tam giác ABC cân tại A nên AC = AB = $\large \sqrt{34}$ cm.

Bài 9.21

Áp dụng định lí Pythagore cho tam giác ABC vuông tại B ta có: AB2 + BC2 = AC2.

Suy ra BC2 = AC2 - AB2 = 172 - 82 = 225.

Do đó, BC = 15 (cm).

Diện tích của hình chữ nhật là: AB . BC = 8 . 15 = 120 (cm2)

Bài 9.22

- Áp dụng định lí Pythagore cho tam giác ABE vuông tại B, có

AE2 = AB2 + BE2 = 52 + 32 = 34.

Suy ra AE = $\large \sqrt{34}$ m < 6 m.

Suy ra chú cún có thể chạy đến điểm E do khoảng cách AE ngắn hơn sợi dây.

- Áp dụng định lí Pythagore cho tam giác ADF vuông tại D, có

AF2 = AD2 + DF2 = 52 + 42 = 41.

Suy ra AE = $\large \sqrt{41}$ m > 6 m.

Suy ra chú cún không thể chạy đến điểm F do khoảng cách AF dài hơn sợi dây.

- Áp dụng định lí Pythagore cho tam giác ADC vuông tại D, có

AC2 = AD2 + DC2 = 52 + 52 = 50.

Suy ra AE = 5 $\large \sqrt{2}$ m > 6 m.

Suy ra chú cún không thể chạy đến điểm C do khoảng cách AC dài hơn sợi dây.

Vậy chú cún không thể chạy hết tất cả các điểm của mảnh vườn. Chú chó chỉ có thể chạy đến điểm B, D, E.

4.2 Bài tập về định lý pythagore toán 8 chân trời sáng tạo

Bài 1

a) Áp dụng định lí Pythagore cho tam giác ABC vuông tại A, ta có:

BC2 = AB2 + AC2 = 72 + 242 = 49 + 576 = 625 = 252.

Vậy BC = 25 cm.

b) Áp dụng định lí Pythagore cho tam giác ABC vuông tại A, ta có:

BC2 = AB2 + AC2.

Suy ra AB2 = BC2 - AC2 = $\large (\sqrt{13})^{2}$ - 22 = 13 - 4 = 9 = 32.

Vậy AB = 3 cm.

c) Áp dụng định lí Pythagore cho tam giác ABC vuông tại A, ta có:

BC2 = AB2 + AC2.

Suy ra: AC2 = BC2 - AB2 = 252 - 152 = 625 - 225 = 400 = 202.

Vậy AC = 20 cm.

Bài 2

Đặt các điểm A, B, C như hình vẽ trên.

Áp dụng định lí Pythagore cho tam giác ABC vuông tại A, ta có:

BC2 = AB2 + AC2.

Suy ra: AC2 = BC2 - AB2 = 502 - 252 = 2 500 - 625 = 1 875 .

Do đó AC = $\large \sqrt{1875}$ (m).

Độ cao của con diều so với mặt đất là:

1 + $\large \sqrt{1875}$ $\large \approx 44,3$ (m).

Vậy độ cao của con diều so với mặt đất khoảng 44,3 m.

Bài 3

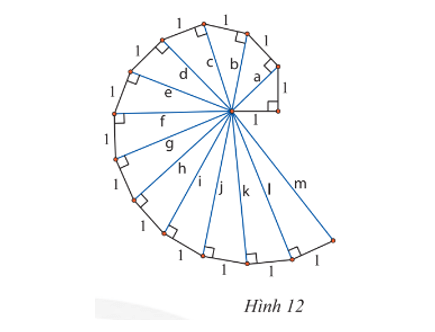
Định lí Pythagore và ứng dụng| Toán 8 chương trình mới

Áp dụng định lí Pythagore lần lượt cho các tam giác vuông có cạnh huyền a, b, c, d trong Hình 12 ta có:

• a2 = 12 + 12 = 2, suy ra a = $\large \sqrt{2}$ ;

• b2 = a2 + 12 = 2 + 1 = 3, suy ra b = $\large \sqrt{3}$ .

• c2 = b2 + 12 = 3 + 1 = 4, suy ra c = $\large \sqrt{4}$ = 2.

• d2 = c2 + 12 = 4 + 1 = 5, suy ra d = $\large \sqrt{5}$ .

Dự đoán kết quả của các cạnh huyền còn lại:

e = $\large \sqrt{6}$ ; f = $\large \sqrt{7}$ ; g = $\large \sqrt{8}$ ; h = $\large \sqrt{9}$ = 3; i = $\large \sqrt{10}$ ; j = $\large \sqrt{11}$ ; k = $\large \sqrt{12}$ ; l = $\large \sqrt{13}$ ; m = $\large \sqrt{14}$ .

Bài 4

a) Ta có: 172 = 82 + 152. Suy ra BC2 = AB2 + AC2.

Vậy tam giác ABC vuông tại A.

b) Ta có 292 = 202 + 212. Suy ra AB2 = BC2 + AC2.

Vậy tam giác ABC vuông tại C.

c) Ta có 372 = 122 + 352. Suy ra AC2 = AB2 + BC2.

Vậy tam giác ABC vuông tại B.

Bài 5

Đặt các điểm A, B, C, H như hình vẽ trên.

Áp dụng định lí Pythagore cho tam giác ABC vuông tại C, ta có:

AB2 = AC2 + BC2.

Suy ra: AC2 = AB2 - BC2 = 132 - 52 = 169 - 25 = 144 = 122.

Do đó AC = 12 m và AH = 12 + 3 = 15 (m).

Vậy chiều cao mà thang có thể vươn tới là 15 m.

Bài 6

Đặt các điểm A, B lần lượt là vị trí của đỉnh tháp hải đăng, chân tháp hải đăng và C là vị trí của con thuyền.

Áp dụng định lí Pythagore cho tam giác ABC vuông tại B, ta có:

AC2 = AB2 + BC2 = 252 + 1802 = 625 + 32 400 = 33 025.

Suy ra AC ≈ 181,73 (m).

Vậy khoảng cách từ thuyền đến ngọn hải đăng khoảng 181,73 m.

4.3 Bài tập về định lý pythagore toán 8 cánh diều

Bài 1

Do tam giác ABC vuông tại A nên theo định lí Pythagore ta có:

BC2 = AB2 + AC2 (1)

a) Từ (1) suy ra AC2 = BC2 - AB2 = 172 - 82 = 289 - 64 = 225 = 152

Do đó AC = 15 (cm).

b) Từ (1) suy ra BC2 = 202 + 212 = 400 + 441 = 841 = 292

Do đó BC = 29 (cm).

c) Từ (1) suy ra BC2 = 62 + 62 = 36 + 36 = 72

Do đó: $\large BC=\sqrt{72}=\sqrt{36.2}=6\sqrt{2}$

Bài 2

a) Ta có: 122 + 352 = 144 + 1 225 = 1 369 và 372 = 1 369.

Suy ra 122 + 352 = 372

Do đó theo định lí Pythagore đảo, tam giác có độ dài ba cạnh 12 cm, 35 cm, 37 cm là tam giác vuông.

b) Ta có: 72 + 82 = 49 + 64 = 113 và 102 = 100.

Suy ra 72 + 82 ≠ 102.

Do đó tam giác có độ dài ba cạnh 10 cm, 7 cm, 8 cm không phải là tam giác vuông.

c) Ta có: 62 + 72 = 36 + 49 = 85 và 112 = 121.

Suy ra 62 + 72 ≠ 112.

Do đó tam giác có độ dài ba cạnh 11 cm, 6 cm, 7 cm không phải là tam giác vuông.

Bài 3

Do tam giác đã cho là tam giác vuông cân nên độ dài hai cạnh góc vuông cùng bằng 1 dm

Khi đó theo định lí Pythagore, độ dài cạnh huyền của tam giác vuông cân đó là:

$\large \sqrt{1^{2}+1^{2}}=\sqrt{2} (dm)$

Bài 4

a) Vẽ đường cao AH của tam giác đều ABC.

Khi đó H là trung điểm của BC nên HB = HC = 1/2a.

Xét tam giác AHC vuông tại H, theo định lí Pythagore ta có:

AC2 = AH2 + HC2

Suy ra AH2 = AC2 - HC2

$\large =a^{2}-\left ( \frac{1}{2}a \right )^{2}=a^{2}-\frac{1}{4}a^{2}=\frac{3}{4}a^{2}=\left ( \frac{\sqrt{3}}{2} \right )^{2}.a^{2}=\left ( \frac{a\sqrt{3}}{2} \right )^{2}$

Do đó: $\large AH=\frac{a\sqrt{3}}{2}$

b) Diện tích của tam giác ABC là:

$\large S=\frac{1}{2}AH.BC=\frac{1}{2}.\frac{a\sqrt{3}}{2}=\frac{a^{2}\sqrt{3}}{4}$

Bài 5

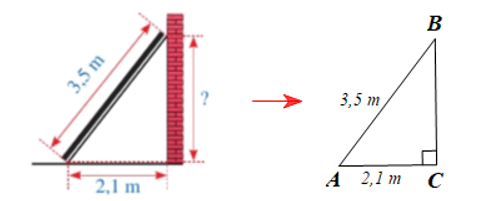
Định lí Pythagore và ứng dụng| Toán 8 chương trình mới

Xét tam giác ABC vuông tại C, theo định lí Pythagore ta có:

AB2 = AC2 + BC2

Suy ra BC2 = AB2 - AC2 = 3,52 - 2,12 = 12,25 - 4,41 = 7,84 = 2,82

Do đó BC = 2,8 m.

Vậy khoảng cách từ điểm thanh gỗ chạm vào tường đến mặt đất là 2,8 mét.

Bài 6

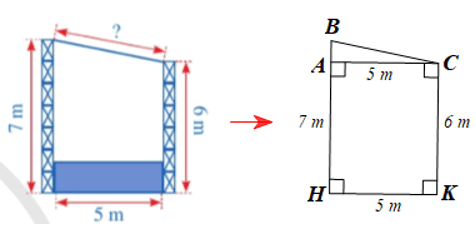
Định lí Pythagore và ứng dụng| Toán 8 chương trình mới

Ta có: AB = BH - AH = BH - CK = 7 - 6 = 1 (m).

Xét tam giác ABC vuông tại A, theo định lí Pythagore ta có:

BC2 = AB2 + AC2 = 12 + 52 = 1 + 25 = 26.

$\large \Rightarrow BC=\sqrt{26}=5,09901\approx 5,10(m)$

Vậy chiều dài của mái che sân khấu đó khoảng 5,10 mét.

Trên đây là lý thuyết Định lý pythagore toán 8 chi tiết cùng hướng dẫn giải bài tập cuối sách toán 8 kết nối tri thức, chân trời sáng tạo và cánh diều. Tham khảo thêm các bài học khác trong chương trình toán 8 tại trang web vuihoc.vn bạn nhé!

>> Mời bạn tham khảo thêm:

Cách tính xác suất của biến cố bằng tỉ số
Hai tam giác đồng dạng
Ba trường hợp đồng dạng của hai tam giác