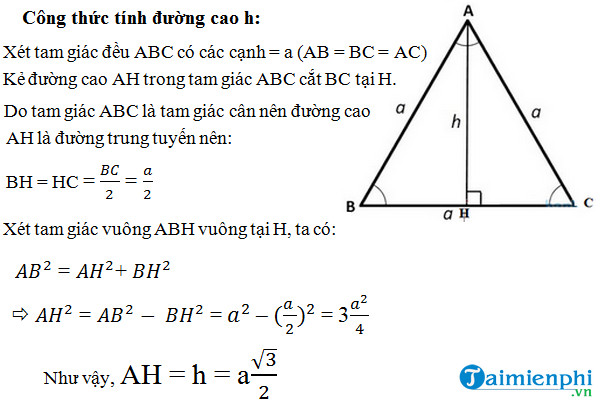
Trong tam giác cân, đường cao kẻ từ đỉnh xuống cạnh đáy chính là đường phân giác và trung tuyến của cạnh đó. Để tính đường cao trong tam giác cân, chúng ta áp dụng định lý Pythagoras trong tam giác vuông mới tạo bởi đường cao.
Công Thức Tính Đường Cao
Công thức tính đường cao \( h \) từ đỉnh của tam giác cân xuống cạnh đáy là:
$$h = \sqrt{a^2 - \left(\frac{b}{2}\right)^2}$$
Trong đó:
- \( h \) là chiều cao từ đỉnh xuống cạnh đáy.
- \( a \) là độ dài cạnh bên của tam giác cân.
- \( b \) là độ dài cạnh đáy.
Ví Dụ Minh Họa
Cho tam giác ABC cân tại A, với AB = AC = 5 cm, BC = 6 cm. Để tính đường cao AH, ta làm như sau:
- Kẻ đường cao AH từ đỉnh A xuống cạnh đáy BC, AH vuông góc với BC và chia BC thành hai đoạn bằng nhau, BH = HC = 3 cm.
- Áp dụng định lý Pythagoras cho tam giác ABH: $$ AH^2 + BH^2 = AB^2 $$
- Thay số vào, ta có: $$ AH^2 + 3^2 = 5^2 $$
- Tính được: $$ AH^2 = 25 - 9 = 16 \implies AH = 4 \text{ cm} $$
Bài Tập Thực Hành
Dưới đây là một số bài tập về tính đường cao trong tam giác cân:
Bài Tập Đề Bài Lời Giải Bài Tập 1 Cho tam giác ABC cân tại A có độ dài hai cạnh AB = AC = 4 cm, BC = 14 cm. Tính chiều dài đường cao trong tam giác cân ABC. Kẻ đường cao AH vuông góc với BC tại H. Vì đường cao tam giác cân đi qua trung điểm của cạnh đáy nên BH = HC = BC/2 = 14/2 = 7 cm. Áp dụng công thức trên: $$ AH^2 + BH^2 = AB^2 \implies AH^2 = AB^2 - BH^2 = 16 - 49 = -33 $$ Do dữ liệu sai. Bài Tập 2 Cho tam giác DEF cân tại D, với DE = DF = 10 cm, EF = 24 cm. Tính chiều dài đường cao DI. Kẻ đường cao DI vuông góc với EF tại trung điểm, do đó EI = IF = 12 cm. Áp dụng định lý Pythagoras: $$ DI^2 + EI^2 = DE^2 \implies DI^2 = 10^2 - 12^2 = 100 - 144 = -44 $$ Do dữ liệu sai.Ứng Dụng Thực Tiễn
Đường cao trong tam giác cân giúp chúng ta tính toán chính xác diện tích và các tính chất hình học khác của tam giác. Sử dụng công thức này là một bước quan trọng trong việc giải quyết các bài toán liên quan đến hình học và ứng dụng thực tế.