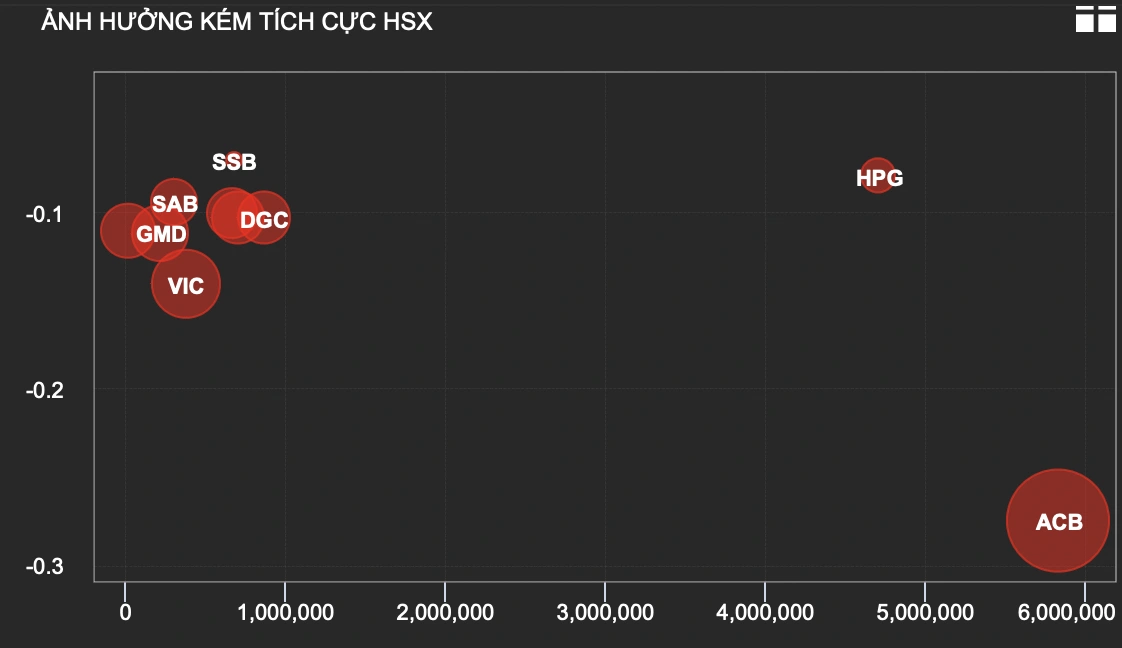
Khi nghiên cứu về hình thang, đường trung bình là một kiến thức quan trọng ứng dụng cho nhiều bài toán và thực tế. Qua bài viết dưới đây, Cmath sẽ cùng các em học sinh tìm hiểu chi tiết về đường trung bình của hình thang và bài tập áp dụng đi kèm nhé!
Đường trung bình của hình thang là gì?
Đường trung bình của hình thang là đoạn thẳng nối trung điểm hai cạnh bên của hình thang. Nghĩa là nếu có một hình thang và bạn nối hai điểm chính giữa của hai cạnh bên lại với nhau, đoạn thẳng vừa vẽ được gọi là đường trung bình của hình thang.

Tính chất quan trọng nhất của đường trung bình hình thang:
- Song song với hai đáy: Đường trung bình luôn song song với hai đáy của hình thang. Điều này có nghĩa là nó sẽ không bao giờ cắt ngang hai đáy.
- Bằng nửa tổng hai đáy: Độ dài của đường trung bình bằng một nửa tổng độ dài hai đáy của hình thang.
Công thức tính đường trung bình của hình thang
Đường trung bình của hình thang là một khái niệm quan trọng trong hình học, nó đại diện cho đoạn thẳng nối trung điểm của hai cạnh bên của hình thang.
Công thức đường trung bình rất đơn giản: Đường trung bình = (Đáy lớn + Đáy nhỏ) : 2
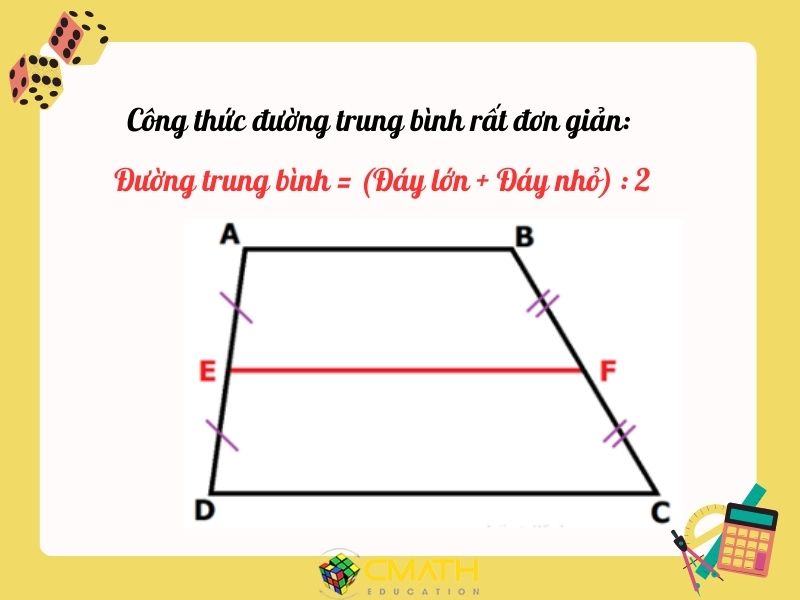
Giả sử hình thang ABCD có AB và CD là hai đáy, EF là đường trung bình (với E là trung điểm của AD, F là trung điểm của BC). Khi đó, ta có công thức tính độ dài đường trung bình EF như sau: EF = (AB + CD) / 2
Trong đó:
- EF: Độ dài đường trung bình.
- AB: Độ dài đáy nhỏ.
- CD: Độ dài đáy lớn.
Nhờ tính chất đặc biệt này, ta có thể dễ dàng tính được độ dài của đường trung bình hoặc độ dài của một đáy khi biết các thông số còn lại. Đặc biệt, đường trung bình thường xuất hiện trong các bài toán về hình thang, giúp chúng ta giải quyết các bài toán liên quan đến diện tích, chu vi hoặc chứng minh các tính chất hình học.
Ứng dụng của đường trung bình trong thực tế
Đường trung bình của hình thang không chỉ là một khái niệm lý thuyết trong hình học mà còn có rất nhiều ứng dụng thực tế vô cùng hữu ích, cụ thể như:
- Kiến trúc và xây dựng: Đường trung bình được sử dụng để tính toán độ dài trong xây dựng mái nhà có dạng hình thang. Việc xác định chính xác độ dài này giúp đảm bảo mái nhà vững chắc và cân đối.
- Thiết kế nội thất: Trong thiết kế nội thất, đường trung bình được ứng dụng để tạo ra các hình dạng đối xứng và cân bằng, tạo cảm giác hài hòa cho không gian.
- Đo đạc và khảo sát: Khi không thể đo trực tiếp khoảng cách giữa hai điểm, người ta có thể sử dụng tính chất của đường trung bình để tính toán gián tiếp.
- Cơ khí: Đường trung bình được sử dụng để tính toán kích thước các chi tiết máy, đảm bảo các bộ phận hoạt động trơn tru và chính xác.
- Nghệ thuật và thiết kế: Đường trung bình được sử dụng để tạo ra các hình dạng đối xứng và cân bằng trong thiết kế logo, poster, và các sản phẩm đồ họa khác.
Tổng hợp các dạng bài tập thường gặp về đường trung bình của hình thang
Các dạng bài tập về đường trung bình của hình thang thường gặp ở cấp THCS và THPT. Dưới đây là một số dạng bài tập phổ biến được ứng dụng trong toán học:
Dạng 1: Xác định và chứng minh đường trung bình
Nhiệm vụ của bài tập này là tìm ra và chứng minh một đoạn thẳng đặc biệt có tên là “đường trung bình”. Để làm được điều này, ta cần vận dụng định nghĩa và tính chất của đường trung bình một cách thành thạo. Đây là bước đầu tiên giúp chúng ta làm quen và hiểu rõ hơn về khái niệm đường trung bình.
Dạng 2: Tính toán với đường trung bình
Sau khi đã làm quen với đường trung bình, ta sẽ bước sang giai đoạn vận dụng những kiến thức đã học để giải quyết các bài toán tính toán. Đó có thể là tính độ dài của đường trung bình, tính diện tích của các hình liên quan hoặc tìm mối quan hệ giữa các yếu tố hình học khác nhau. Các bài toán này giúp chúng ta rèn luyện kỹ năng tính toán và khả năng tư duy logic.
Dạng 3: Kết hợp đường trung bình của tam giác và hình thang
Đây là dạng bài tập nâng cao, đòi hỏi chúng ta phải kết hợp kiến thức về đường trung bình của cả tam giác và hình thang. Các bài toán này thường phức tạp hơn và đòi hỏi tư duy linh hoạt để tìm ra cách giải phù hợp. Việc giải quyết các bài toán dạng này không chỉ giúp chúng ta nắm vững kiến thức mà còn rèn luyện khả năng tư duy trừu tượng và sáng tạo.
Một số bài tập về đường trung bình của hình thang tự luyện tại nhà
Bài 1: Cho hình thang ABCD (AB // CD). Gọi M, N lần lượt là trung điểm của AD và BC. Tính độ dài MN biết AB = 8cm, CD = 12cm.
Bài 2: Cho hình thang ABCD (AB // CD). Gọi M, N lần lượt là trung điểm của AD và BC. Chứng minh rằng MN song song với AB và CD, đồng thời MN = 1/2(AB + CD).
Bài 3: Cho hình thang ABCD (AB // CD), có AB = 6cm, CD = 10cm. Gọi M là trung điểm của AD, N là trung điểm của BC. Tính độ dài MN.
Bài 4: Cho hình thang cân ABCD (AB // CD). Gọi M, N lần lượt là trung điểm của AD và BC. Chứng minh rằng tứ giác ABNM là hình thang cân.
Bài 5: Cho hình thang ABCD (AB // CD), có AB = 8cm, CD = 12cm. Gọi M, N lần lượt là trung điểm của AD và BC. Tính diện tích hình thang ABNM biết diện tích hình thang ABCD là 60 cm².
Bài 6: Cho hình thang ABCD (AB // CD), có AB = 6cm, CD = 10cm. Gọi M là trung điểm của AD, N là trung điểm của BC. Tính độ dài đoạn thẳng MN biết AC = 8cm, BD = 10cm.
Bài 7: Cho hình thang ABCD (AB // CD). Gọi M, N lần lượt là trung điểm của AD và BC. Đường thẳng MN cắt BD tại E, cắt AC tại F. Chứng minh rằng ME = NF.
Bài 8: Cho hình thang cân ABCD (AB // CD), có AB = 8cm, CD = 12cm. Gọi M, N lần lượt là trung điểm của AD và BC. Kẻ BH vuông góc với CD tại H. Tính độ dài BH biết MN = 10cm.
Bài 9: Cho hình thang ABCD (AB // CD), có AB = 6cm, CD = 10cm. Gọi M là trung điểm của AD, N là trung điểm của BC. Đường thẳng MN cắt BD tại E, cắt AC tại F. Chứng minh rằng EF // AB.
Bài 10: Cho hình thang ABCD (AB // CD), có AB = 8cm, CD = 12cm. Gọi M, N lần lượt là trung điểm của AD và BC. Đường thẳng MN cắt BD tại E, cắt AC tại F. Tính độ dài EF biết AB = 10cm, CD = 14cm.
Cmath - Câu lạc bộ Toán học muôn màu cùng các em chinh phục bài tập khó, đạt điểm cao
Cmath là một trong những CLB giảng dạy toán học uy tín, chất lượng luôn được phụ huynh tin tưởng lựa chọn. Với hơn 10 năm kinh nghiệm giảng dạy, Cmath ngày càng cải tiến với chất lượng giảng dạy tốt, truyền cảm hứng giúp các em học sinh làm chủ kiến thức, khơi dậy tiềm năng.

Khi tham gia học tập tại Cmath các em học sinh sẽ nhận được những lợi ích như:
- Chương trình học đa dạng: Kết hợp hài hòa giữa chương trình toán trong nước và quốc tế, giúp học sinh tiếp cận với những kiến thức mới mẻ và phương pháp giải bài đa dạng.
- Giáo trình sáng tạo: Bài tập được thiết kế để kích thích tư duy, không rập khuôn, giúp học sinh chủ động khám phá và tìm tòi.
- Phân lớp học sinh linh hoạt: Cmath phân đều lớp, nhằm đảm bảo mỗi học sinh đều được học tập trong môi trường chất lượng, phù hợp với năng lực của mình.
- Thầy cô tận tâm: Đội ngũ giáo viên tại Cmath có chuyên môn cao, giàu kinh nghiệm, nhiệt huyết, luôn sẵn sàng hỗ trợ học sinh.
- Theo dõi sát sao tiến độ học tập: CLB thường xuyên đánh giá, phản hồi và điều chỉnh kế hoạch học tập cho từng học sinh
Cmath không chỉ là một câu lạc bộ toán học đơn thuần mà còn là một ngôi nhà chung của những bạn trẻ yêu thích toán học. Với phương pháp giảng dạy hiện đại và đội ngũ giáo viên tận tâm, Cmath tự hào là nơi giúp các em học sinh phát triển toàn diện về kiến thức và kỹ năng Toán học, đặc biệt là bài tập nâng cao về đường trung bình của hình thang. Liên hệ ngay với Cmath để nhận được sự hỗ trợ nhanh chóng nhé!
Xem thêm:
- Trung tâm bồi dưỡng toán hình học tốt nhất tại Hà Nội | Cmath
- Toán tư duy là gì? Có nên cho trẻ học Toán tư duy từ sớm?
- Tư duy logic là gì? Bí quyết rèn luyện tư duy logic cho trẻ