1. Định nghĩa xác suất có điều kiện
- Định nghĩa: Cho hai biến cố A và B. Xác xuất của biến cố A với điều kiện biến cố B xảy ra được gọi là xác suất của A với điều kiện của B, kí hiệu là P(A|B). Nếu P(B) > 0 thì:
$\large P(A|B)=\frac{P(A\cap B)}{P(B)}$
2. Công thức tính xác suất có điều kiện
- Cho A và B là hai biến cố, trong đó P(B) > 0. Khi đó:
$\large P(A|B)=\frac{P(A\cap B)}{P(B)}$
- Chú ý:
+ Ta cũng kí hiệu biến cố giao của hai biến cố A và B là AB.
+ Trong thực tế, người ta thường dùng tỉ lệ phần trăm để mô tả xác suất. Chẳng hạn phát biểu "khả năng xảy ra một sự kiện là 20%" cũng có nghĩa là "xác suất xảy ra sự kiện đó là 0,2", phát biểu "tỉ lệ phế phẩm của một lô hàng là 5%" cũng có nghĩa là "nếu chọn ra ngẫu nhiên 1 sản phẩm từ lô hàng, xác suất sản phẩm đó là phế phẩm là 0,05".
+ Với P(B) > 0, ta có: $\large P(AB)= P(B)P(A/B)$
+ Với A và B là hai biến cố bất kì thì: $\large P(AB)= P(B)P(A/B)$ ( công thức nhân xác suất cho hau biến cố)
+ Với mọi biến cố A và B, trong đó P(B) > 0, ta có: $\large P(\overline{A}|B)=1-P(A|B)$
+ Với A và B là hai biến cố độc lập, trong đó 0 < P(B) < 1, người ta chứng minh được rằng:
$\large P(A|B)=P(A|\overline{B})=P(A)$
Từ đẳng thức trên, ta thấy khi A và B độc lập thì việc biến cố B xảy ra hay không xảy ra không làm ảnh hưởng đến xác suất của biến cố A.
3. Sơ đồ hình cây
- Trên sơ đồ hình cây:
+ Xác suất của xác nhánh trong sơ đồ hình cây từ đỉnh thứ hai là xác suất có điều kiện.
+ Xác suất xảy ra của mỗi kết quả bằng tích các xác suất trên các nhánh của cây đi đến kết quả đó.
- Ví dụ: Bạn Việt chuẩn bị đi tham quan một hòn đảo trong hai ngày thứ Bảy và Chủ nhật. Ở hòn đảo đó, mỗi ngày chỉ có nắng hoặc mưa, nếu một ngày là nắng thì khả năng xảy ra mưa ở ngày tiếp theo là 20%, còn nếu một ngày là mưa thì khả năng ngày hôm sau vẫn mưa là 30%. Theo dự báo thời tiết, xác suất trời sẽ nắng vào thứ Bảy là 0,7. Hãy tìm các giá trị thích hợp thay vào ? ở sở đồ hình cây sau:
Đáp án:

4. Bài tập về xác suất có điều kiện toán 12
4.1 Bài tập về xác suất có điều kiện toán 12 kết nối tri thức
Bài 6.1 trang 70 sgk toán 12/2 kết nối tri thức
Gọi A là biến cố: “Người đó rút được thẻ số 10”;
B là biến cố: “Người đó rút được thẻ mang số chẵn”.
Ta có AB = {10}; B = {2; 4; 6; 8; 10; 12; 14; 16; 18; 20}.
Khi đó: $\large P(AB)=\frac{1}{20}; P(B)=\frac{10}{20}$
Vậy: $\large P(A|B)=\frac{P(AB)}{P(B)}=\frac{1}{10}$
Bài 6.2 trang 70 sgk toán 12/2 kết nối tri thức
Áp dụng công thức nhân xác suất, ta có: P(AB) = P(A) ∙ P(B | A) = 0,2 ∙ 0,8 = 0,16.
$\large \Rightarrow P(A|B)=\frac{P(AB)}{B}=\frac{0,16}{0,51}\approx 0,3137$
Bài 6.3 trang 70 sgk toán 12/2 kết nối tri thức
Gọi A là biến cố: “Tổng số chấm xuất hiện trên hai con xúc xắc bằng 7”;
B là biến cố: “Có ít nhất một con xúc xắc xuất hiện mặt 5 chấm”.
a) Cần tính P(A | B).
Ta có n(Ω) = 36; AB = {(2; 5); (5; 2)} ⇒ n(AB) = 2
$\large \Rightarrow P(AB)=\frac{2}{36}$
$\large \Rightarrow \overline{B}$={(a; b) | a, b ∈ {1; 2; 3; 4; 6}} ⇒ n( $\large \overline{B}$)= 5 ∙ 5 = 25.
$\large \Rightarrow P(\overline{B})=\frac{25}{36}\Rightarrow P(B)=1-P(\overline{B})=1-\frac{25}{36}=\frac{11}{36}$
$\large \Rightarrow P(A|B)=\frac{P(AB)}{P(A)}=\frac{2}{11}$
b) Ta cần tính P(B| A).
Ta có $\large \Rightarrow P(B|A)=\frac{P(AB)}{P(A)}$ Ở câu a) ta đã có P(AB) = 2/36. Cần tính P(A).
Ta có A = {(1; 6); (2; 5); (3; 4); (4; 3); (5; 2); (6; 1)}; n(A) = 6 => P(A) = 6/36
Ta có $\large \Rightarrow P(B|A)=\frac{P(AB)}{P(A)}=\frac{2}{6}=\frac{1}{3}$
Đăng ký ngay combo sổ tay kiến thức các môn học để nhận ưu đãi cực hấp dẫn từ vuihoc nhé!

Bài 6.4 trang 70 sgk toán 12/2 kết nối tri thức
Gọi A là biến cố: “tổng số chấm xuất hiện trên hai con xúc xắc đó không nhỏ hơn 10”;
B là biến cố: “ít nhất một con xúc xắc xuất hiện mặt 5 chấm”.
Cần tính P(A|B).P(A|B).
Ta có AB = {(5; 5); (5; 6); (6; 5)}; n(AB) = 3 $\large \Rightarrow P(AB)=\frac{3}{36}$
$\large \Rightarrow \overline{B}$= {(a; b) | a, b ∈ {1; 2; 3; 4; 6}} ⇒ n($\large \Rightarrow \overline{B}$) = 5 ∙ 5 = 25.
$\large \Rightarrow P(\overline{B})=\frac{25}{36}\Rightarrow P(B)=1-P(\overline{B})=1-\frac{25}{36}=\frac{11}{36}$
$\large \Rightarrow P(A|B)=\frac{P(AB)}{P(B)}=\frac{3}{11}$
Bài 6.5 trang 70 sgk toán 12/2 kết nối tri thức
a) Gọi A là biến cố: “Thí nghiệm thứ nhất thành công” và B là biến cố: “Thí nghiệm thứ hai thành công”. Khi đó biến cố “Cả hai thí nghiệm đều thành công” là AB.
Theo công thức nhân xác suất ta có P(AB) = P(A).P(B| A).
Theo bài ra ta có P(A) = 0,7; P(B | A) = 0,9.
Thay vào ta được P(AB) = 0,7 ∙ 0,9 = 0,63.
b) Biến cố: “Cả hai thí nghiệm đều không thành công” là $\large \overline{A}\overline{B}$
Theo công thức nhân xác suất ta có $\large P\overline{A}\overline{B}=P(\overline{A}).P(\overline{B}|\overline{A}))$
Ta có $\large P(\overline{B}|\overline{A}))$ là xác suất để thí nghiệm thứ hai không thành công nếu thí nghiệm thứ nhất không thành công. Do đó, từ dữ kiện của bài toán ta có:
$\large P(\overline{B}|\overline{A}))=1-0,4=0,6$
$\large P(\overline{A})=1-P(A)=1-0,7=0,3$
Vậy $\large P(\overline{A}\overline{B})=0,3.0,6=0,18$
Bài 6.6 trang 70 sgk toán 12/2 kết nối tri thức
Gọi A là biến cố: “Lần 1 Hà lấy được kẹo màu cam”;
B là biến cố: “Lần 2 Hà lấy được kẹo màu cam”.
Khi đó AB là biến cố: “Cả hai lần Hà lấy được kẹo màu cam”. Ta có: $\large P(AB)=\frac{1}{3}$
Gọi n là số kẹo ban đầu trong túi (n > 0).
Ta có: $\large P(A)=\frac{6}{n}; P(B|A)=\frac{5}{n-1}$
Theo công thức nhân xác suất, ta có: P(AB) = P(A).P(B | A)
$\large =\frac{6}{n}=\frac{5}{n-1}=\frac{30}{n^{2}-n}=\frac{1}{3}$
⇒ n2 - n - 90 = 0 ⇔ n = - 9 (loại) hoặc n = 10 (t/m).
Vậy ban đầu trong túi có 10 cái kẹo.
4.2 Bài tập về xác suất có điều kiện toán 12 chân trời sáng tạo
Bài 1 trang 75 sgk toán 12/2 chân trời sáng tạo
Gọi A là biến cố “Sách được chọn là sách khoa học tự nhiên”,
B là biến cố “Sách được chọn là quyển sách về khoa học”.
AB là biến cố “Sách được chọn là sách khoa học và là sách khoa học tự nhiên”
Theo đề ta có P(A) = 0,14; P(B) = 0,35; P(AB) = P(A) = 0,14.
$\large \Rightarrow P(A|B)=\frac{P(AB)}{P(B)}=\frac{0,14}{0,35}=0,4$
Bài 2 trang 75 sgk toán 12/2 chân trời sáng tạo
Có $\large P(\overline{B})$ = 1 - P(B) = 0,2.
Theo công thức nhân xác suất ta có:
$\large P(A\overline{B})=P(\overline{B}).P(A|\overline{B}))=0,2.0,5=0,1$
Vì $\large A\overline{B}$ và AB là hai biến cố xung khắc và $\large A\overline{B}\cup AB=A$
$\large P(AB)=P(A)-P(A\overline{B})=0,4-0,1=0,3$
Do đó: $\large P(A|{B})=\frac{P(AB)}{P(B)}=\frac{0,3}{0,8}=\frac{3}{8}$
Bài 3 trang 75 sgk toán 12/2 chân trời sáng tạo
Gọi M là biến cố “Bạn được chọn là nữ”;
N là biến cố “Bạn được chọn học tiếng Anh”.
Ta có: $\large P(M)=\frac{C_{25}^{1}}{C_{45}^{1}}=\frac{5}{9};P(N|M)=0,6; P(N|\overline{M})=0,7$
$\large \Rightarrow P(\overline{M})=1-P(M)=\frac{4}{9}; P(\overline{N}|M)=1-P(N|M)=0,4$
$\large P(\overline{N}|\overline{M})=1-P(N|\overline{M})=0,3$
Ta có sơ đồ hình cây
Dựa vào sơ đồ hình cây, ta có: $\large P(A)=\frac{2}{15}; P(B)=\frac{1}{3}$
Bài 4 trang 75 sgk toán 12/2 chân trời sáng tạo
Gọi A là biến cố “UPS bị hỏng khi xảy ra sự cố điện”.
B là biến cố “Máy tính bị hỏng”.
Ta có P(A) = 0,02; P(B|A) = 0,1; $\large P(\overline{B}|\overline{A}=1$
$\large \Rightarrow P(\overline{B}|A)=1-P(B|A)=0,9$
Dựa vào sơ đồ cây ta có:
a) $\large \Rightarrow P(\overline{AB})=0,98$
b) P(AB) = 0,002.
Đăng ký ngay để được các thầy cô ôn tập kiến thức và xây dựng lộ trình ôn thi THPT Quốc gia sớm với khóa học PAS THPT!

4.3 Bài tập về xác suất có điều kiện toán 12 cánh diều
Bài 1 trang 95 sgk toán 12/2 cánh diều
Đáp án đúng là: B
Vì A, B là hai biến cố độc lập nên P(A ∩ B) = P(A) ∙ P(B) = 0,8 ∙ 0,25 = 0,2.
$\large \Rightarrow P(A|B)=\frac{P(A\cap B)}{P(B)}=\frac{0,2}{0,25}=0,8$
Bài 2 trang 95 sgk toán 12/2 cánh diều
Đáp án đúng là: D
Xét hai biến cố:
A: “Nhà được chọn có ô tô”;
B: “Nhà được chọn gắn biển số chẵn”.
Khi đó, xác suất nhà được chọn có ô tô, biết rằng nhà đó gắn biển số chẵn, chính là xác suất có điều kiện P(A | B).
Theo bài ra, ta có: $\large P(B)=\frac{60}{100}=0,6; P(A\cap B)=\frac{50}{100}=0,5$
$\large \rightarrow P(A|B)=\frac{P(A\cap B)}{P(B)}=\frac{0,5}{0,6}=\frac{5}{6}$
Bài 3 trang 95 sgk toán 12/2 cánh diều
Đáp án đúng là: C
Xét hai biến cố:
A: “Bạn Nam chọn được máy tính đã cài đặt phần mềm lập trình Python”;
B: “Bạn Nam chọn được máy tính được đánh số lẻ”.
Khi đó, xác suất bạn Nam chọn được máy tính đã cài đặt phần mềm lập trình Python, biết rằng máy tính đó được đánh số lẻ, chính là xác suất có điều kiện P(A | B).
Vì có 40 máy tính được đánh số từ 1 đến 40, mỗi máy đánh 1 số khác nhau nên có 20 máy được đánh số lẻ và 20 máy được đánh số chẵn. Ta có P(B)= 20/40 = 0,5.
Theo bài ra ta có, xác suất chọn được một máy tính đã cài đặt phần mềm lập trình Python được đánh số lẻ là 0,45, tức là P(A ∩ B) = 0,45.
$\large \rightarrow P(A|B)=\frac{P(A\cap B)}{P(B)}=\frac{0,45}{0,5}=\frac{9}{10}$
Bài 4 trang 96 sgk toán 12/2 cánh diều
a) Ta có: $\large \rightarrow P(A|B)=\frac{P(A\cap B)}{P(A)}=\frac{0,4}{0,6}=\frac{2}{3}$
b) Vì A ∩ và A ∩ B là hai biến cố xung khắc và (A ∩ $\large \overline{B}$ ) ∪ (A ∩ B) = A nên theo tính chất của xác suất ta có P(A) = P(A ∩ $\large \overline{B}$ ) + P(A ∩ B).
=> P(A ∩$\large \overline{B}$ ) = P(A) - P(A ∩ B) = 0,6 - 0,4 = 0,2.
c) Ta có: $\large \rightarrow P(\overline{B}|A)=\frac{P(\overline{B}\cap A)}{P(A)}=\frac{0,2}{0,6}=\frac{1}{3}$
Bài 5 trang 96 sgk toán 12/2 cánh diều
Nếu A xảy ra, tức là quả bóng màu xanh được lấy ra ở lần thứ nhất. Vì quả bóng lấy ra được bỏ lại vào hộp nên trong hộp có 3 quả bóng xanh và 4 quả bóng đỏ.
Vậy P(B) = 4/7 .
Nếu A không xảy ra, tức là quả bóng màu đỏ được lấy ra ở lần thứ nhất. Vì quả bóng lấy ra được bỏ lại vào hộp nên trong hộp vẫn có 3 quả bóng xanh và 4 quả bóng đỏ.
Vậy P(B) =4/7 .
Như vậy, xác suất xảy ra của biến cố B không thay đổi bởi việc xảy ra hay không xảy ra của biến cố A.
Vì lần thứ nhất lấy và lần thứ hai lấy sau lần thứ nhất nên P(A) = 3/7 dù biến cố B có xảy ra hay không xảy ra.
Vậy A và B là hai biến cố độc lập.
Bài 6 trang 96 sgk toán 12/2 cánh diều
Xét hai biến cố:
A: “Tổng số chấm xuất hiện trên hai xúc xắc bằng 6”;
B: “Xúc xắc thứ nhất xuất hiện mặt 4 chấm”.
Khi đó, xác suất để tổng số chấm xuất hiện trên hai xúc xắc bằng 6, biết rằng xúc xắc thứ nhất xuất hiện mặt 4 chấm, chính là xác suất có điều kiện P(A | B).
Vì gieo lần lượt từng xúc xắc trong hai xúc xắc đó nên n(Ω) = 6 ∙ 6 = 36.
Xúc xắc thứ nhất xuất hiện mặt 4 chấm thì có 1 cách chọn, xúc xắc thứ hai có 6 cách chọn mặt xuất hiện. Do đó, P(B) = 1/6.
Biến cố A ∩ B: “Tổng số chấm xuất hiện trên hai xúc xắc bằng 6 và xúc xắc thứ nhất xuất hiện mặt 4 chấm”. Khi đó, để có tổng số chấm bằng 6 thì xúc xắc thứ hai phải xuất hiện mặt 2 chấm. Do đó, P(A ∩ B) = 1/36 .
Khi đó, ta có: $\large \rightarrow P(A|B)=\frac{P(A\cap B)}{P(B)}=\frac{\frac{1}{36}}{\frac{1}{6}}=\frac{1}{6}$
Vậy xác suất để tổng số chấm xuất hiện trên hai xúc xắc bằng 6, biết rằng xúc xắc thứ nhất xuất hiện mặt 4 chấm, là 1/6.
Bài 7 trang 96 sgk toán 12/2 cánh diều
Gọi A là biến cố: “chiếc áo sơ mi trong lô hàng S được chọn qua được lần kiểm tra thứ nhất”, B là biến cố: “chiếc áo sơ mi trong lô hàng S được chọn qua được lần kiểm tra thứ hai”, C là biến cố: “chiếc áo sơ mi được chọn đủ tiêu chuẩn xuất khẩu”.
Theo bài ra ta có: P(A) = 98% = 0,98; P(B | A) = 95% = 0,95.
Một chiếc áo đủ tiêu chuẩn xuất khẩu khi cả hai lần kiểm tra chất lượng sản phẩm đều đạt. Xác suất để một chiếc áo sơ mi đủ tiêu chuẩn xuất khẩu là:
P(C) = P(A) ∙ P(B | A) = 0,98 ∙ 0,95 = 0,931.
Bài 8 trang 96 sgk toán 12/2 cánh diều
Xét hai biến cố:
A: “Sản phẩm lấy ra ở lần thứ nhất có chất lượng thấp”;
B: “Sản phẩm lấy ra ở lần thứ hai có chất lượng thấp”.
Khi đó, xác suất để cả hai sản phẩm được lấy ra đều có chất lượng thấp chính là xác suất có điều kiện P(B | A).
Nếu A xảy ra tức là sản phẩm lấy ra ở lần thứ nhất có chất lượng thấp. Khi đó, trong lô sản phẩm còn lại 19 sản phẩm với 4 sản phẩm chất lượng thấp. Vậy P(B | A) = 4/19.
Vậy xác suất để cả hai sản phẩm được lấy ra đều có chất lượng thấp là 4/19.
Bài 9 trang 96 sgk toán 12/2 cánh diều
Vì có 9 quyển sách viết bằng tiếng Anh, trong đó 3 quyển sách Khoa học và 6 quyển sách Nghệ thuật, các quyển sách còn lại viết bằng tiếng Việt nên ta có:
10 + 15 - 9 = 16 quyển sách viết bằng tiếng Việt,
trong đó có 10 - 3 = 7 quyển sách Khoa học và 15 - 6 = 9 quyển sách Nghệ thuật.
Xét hai biến cố sau:
A: “Quyển sách được lấy ra là sách viết bằng tiếng Việt”;
B: “Quyển sách được lấy ra là sách Khoa học”.
Khi đó, xác suất để quyển sách được lấy ra là sách viết bằng tiếng Việt, biết rằng quyển sách đó là sách Khoa học, chính là xác suất có điều kiện P(A | B).
Sơ đồ hình cây biểu thị cách tính xác suất có điều kiện P(A | B), được vẽ như sau:
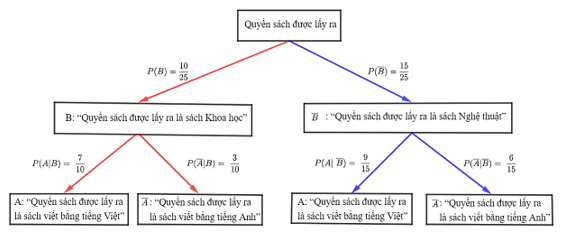
Vậy xác suất để quyển sách được lấy ra là sách viết bằng tiếng Việt, biết rằng quyển sách đó là sách Khoa học, là 0,7
Trên đây là toàn bộ bài học Lý thuyết xác suất có điều kiện toán 12. Hi vọng bài viết này sẽ giúp cho các bạn học sinh hiểu rõ hơn về cách tính xác suất có điều kiện trong chương trình toán 12. Các bạn hãy truy cập nền tảng Vuihoc.vn để ôn tập kiến thức Toán 12 và đăng ký những khóa học bổ ích, hấp dẫn nhất nhé!
>> Mời bạn tham khảo thêm:
- Phương sai và độ lệch chuẩn của mẫu số liệu ghép nhóm toán 12
- Ứng dụng hình học của tích phân trong giải bài tập toán 12
- Công thức tính góc trong không gian toán 12