Tam giác là loại hình học thường gặp không chỉ trong các bài toán mà trong cuộc sống thường ngày. Có 5 loại tam giác bao gồm: tam giác thường, vuông, đều, cân, vuông cân. Vậy tương ứng với các loại tam giác đó, cách tính diện tích hình tam giác sẽ là gì, hãy cùng Dự báo thời tiết tìm hiểu nhé!
Hình tam giác là gì?
Tam giác là gì? - Cách tình diện tích hình tam giác
- Tam giác hay hình tam giác là hình có ba đỉnh là ba điểm không thẳng hàng và ba cạnh là ba đoạn thẳng nối các đỉnh với nhau.
- Tam giác là một đa giác có số cạnh ít nhất (3 cạnh).
- Tam giác là một đa giác đơn và cũng là một đa giác lồi (các góc trong luôn nhỏ hơn 1800).
Cách tình diện tích hình tam giác thường, cân, đều, vuông, vuông cân
Cách tình diện tích hình tam giác
Công thức tính diện tích của một tam giác thường
- Tam giác thường là tam giác cơ bản nhất, có độ dài các cạnh không bằng nhau, số đo góc trong cũng không bằng nhau.
- Có 2 loại tam giác thường: tam giác tù và tam giác nhọn
- Tam giác tù: là tam giác có một góc trong lớn hơn lớn hơn 900(một góc tù) hay có một góc ngoài bé hơn 900 (một góc nhọn).
- Tam giác nhọn: là tam giác có ba góc trong đều nhỏ hơn 900 (ba góc nhọn) hay có tất cả góc ngoài lớn hơn 900 (sáu góc tù).
- Tam giác thường cũng có thể bao gồm các trường hợp đặc biệt khác như tam giác cân, tam giác vuông, tam giác đều. Vì thế, bạn cũng có thể áp dụng 5 công thức tính diện tích tam giác dưới đây để tính diện tích cho nhiều tam giác khác nhau.
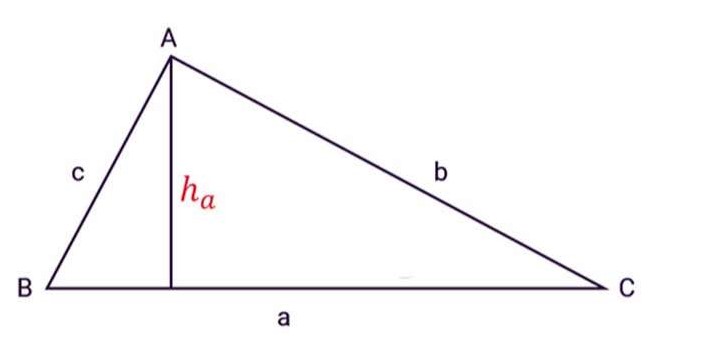
Công thức tính diện tích khi biết độ dài đường cao
- Diện tích tam giác bằng tích của ½ và đường cao hạ từ đỉnh với cạnh đối diện của đỉnh đó.
- Tam giác ABC có ba cạnh là a, b, c và ha là đường cao từ đỉnh A như hình vẽ:
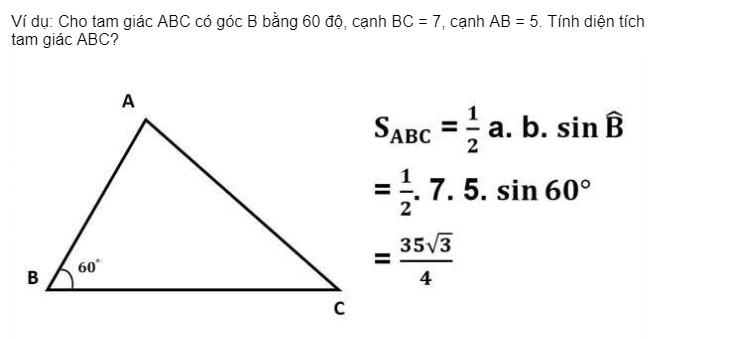
Công thức tính diện tích tam giác khi biết số đo của một góc
Diện tích tam giác bằng ½ tích của hai cạnh kề với sin của góc hợp bởi hai cạnh đó trong tam giác.
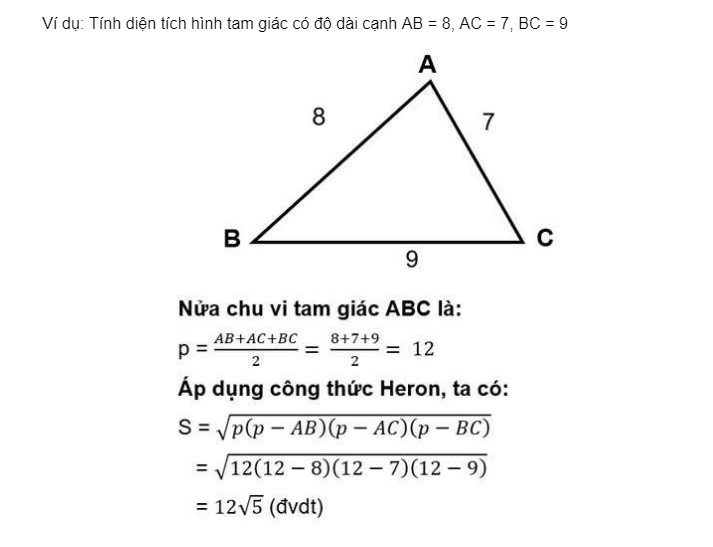
Công thức tính diện tích của một tam giác khi biết 3 cạnh bằng công thức Heron
Một trong 5 công thức tính diện tích tam giác đã được chứng minh và công thức Heron, ta có công thức:
Trong đó:
- a, b, c lần lượt được gọi là độ dài các cạnh của một tam giác.
- p là nửa chu vi tam giác, bằng ½ tổng ba cạnh của một tam giác.
- Với p là nửa chu vi tam giác: p = (a + b + c)/2
Công thức tính diện tích của một tam giác bằng bán kính đường tròn ngoại tiếp và nội tiếp tam giác
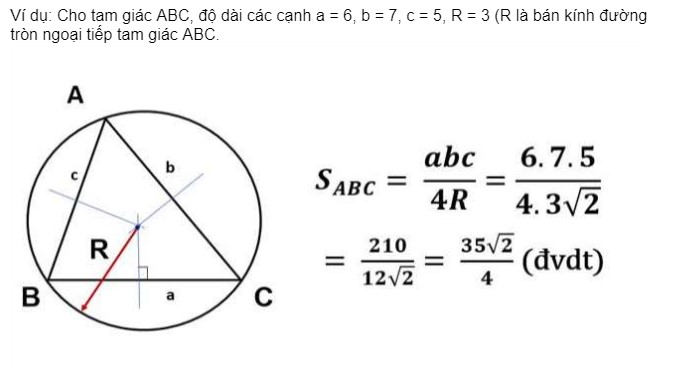
Diện tích của một tam giác bằng bán kính đường tròn ngoại tiếp tam giác (R)
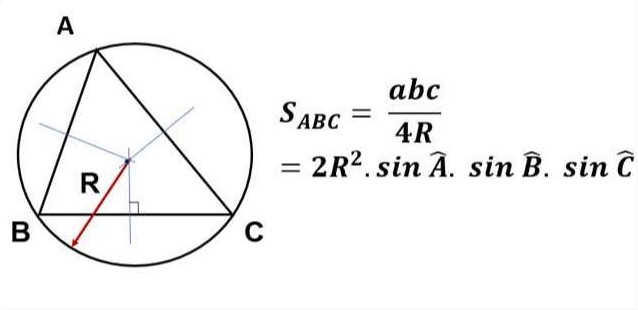Trong đó:
- a, b, c lần lượt được gọi là độ dài các cạnh của một tam giác.
- R là bán kính đường tròn ngoại tiếp của tam giác đó.
- Chú ý: Cần phải chứng minh được R là bán kính đường tròn ngoại tiếp tam giác.
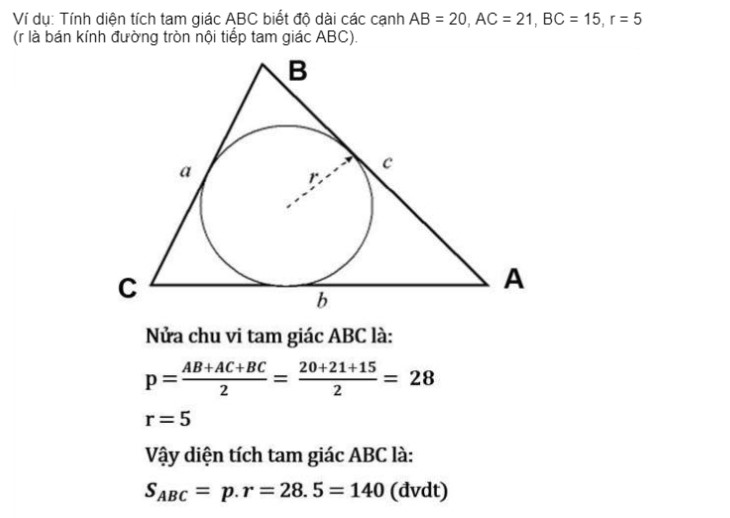
Diện tích tam giác bằng bán kính đường tròn nội tiếp tam giác (r)
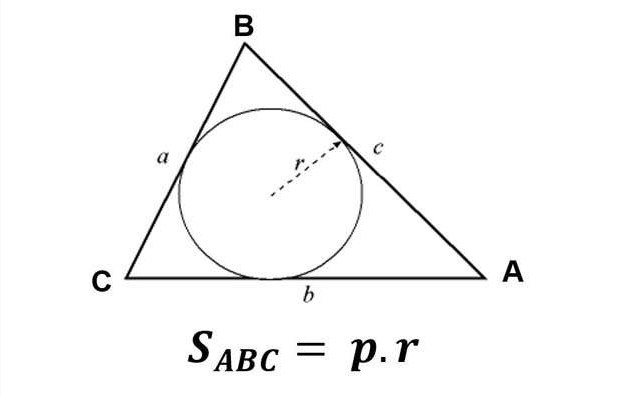Trong đó:
- p là nửa chu vi tam giác.
- r là bán kính đường tròn nội tiếp của tam giác đó
- Gọi r là bán kính đường tròn nội tiếp tam giác ABC và p là nửa chu vi tam giác p=(a+b+c)/2.
Cách tính diện tích hình tam giác trong không gian
Ta có công thức:
Tương tự khi ở trong không gian, với khái niệm tích có hướng của 2 vectơ, ta thấy:
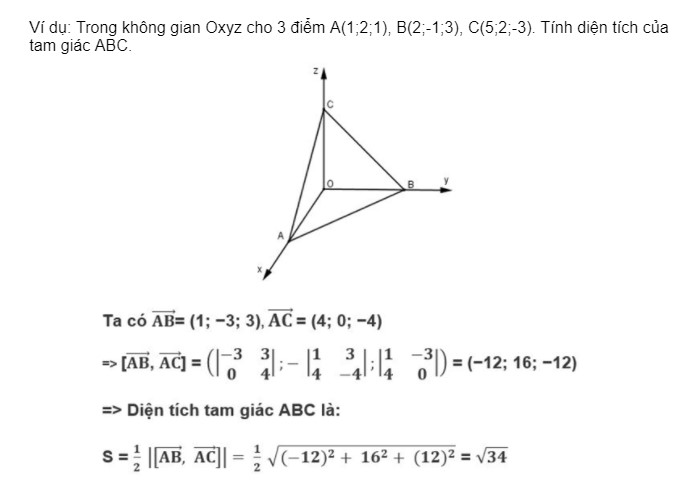
Một số lưu ý khi tính diện tích của một tam giác:
- Với tam giác có chứa góc bẹt và chiều cao nằm bên ngoài tam giác khi đó độ dài cạnh để tính diện tích chính bằng độ dài cạnh trong tam giác đó.
- Khi tính diện tích của một tam giác, chiều cao nào sẽ tương ứng với đáy đó.
- Nếu hai tam giác có chung chiều cao hoặc chiều cao bằng nhau, khi đó diện tích hai tam giác tỉ lệ với 2 cạnh đáy và ngược lại nếu hai tam giác có chung đáy (hoặc hai đáy bằng nhau) -> diện tích tam giác tỉ lệ với 2 đường cao tương ứng.
Công thức tính diện tích của một tam giác cân
- Tam giác cân là tam giác có độ dài hai cạnh bên bằng nhau và số đo hai góc ở đáy cũng bằng nhau.
- Đỉnh của một tam giác cân được tạo thành bởi giao điểm của hai cạnh bên.
- Góc được tạo bởi đỉnh của tam giác cân được gọi là góc ở đỉnh, hai góc còn lại của nó được gọi là hai góc ở đáy.
Tam giác cân ABC có ba cạnh AB, BC, AC, a là độ dài cạnh đáy, b là độ dài hai cạnh bên, ha là đường cao từ đỉnh A như hình vẽ:
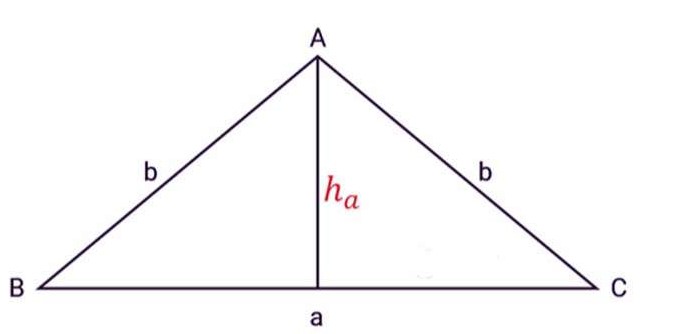Áp dụng công thức tính diện tích của một tam giác thường, ta có công thức tính diện tích tam giác cân như sau:
Công thức tính diện tích của một tam giác đều
- Tam giác được gọi là tam giác đều nếu tam giác có độ dài ba cạnh bằng nhau, số đo các góc cũng bằng nhau và bằng 60 độ.
- Tam giác đều ABC có ba cạnh bằng nhau, a là độ dài các cạnh (AB = BC = AC = a) như hình vẽ:
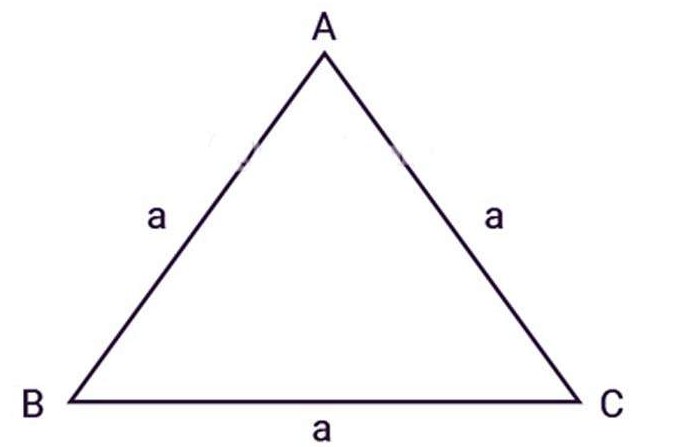Áp dụng định lý Heron để suy ra, ta có công thức tính diện tích của một tam giác đều như sau:
Trong đó:
- a được gọi là độ dài các cạnh của tam giác đều.
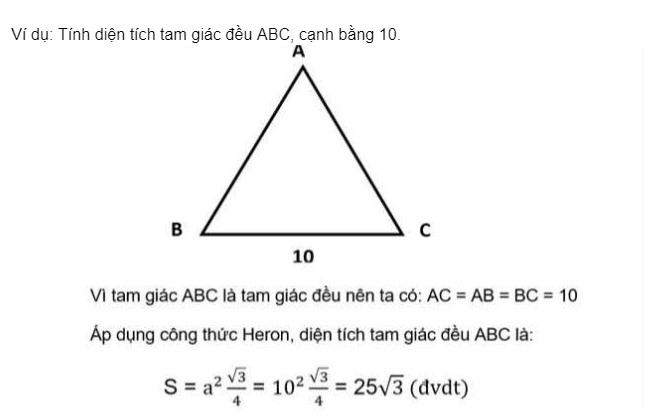
- Ta có ví dụ dưới đây để giúp bạn hiểu hơn về công thức tính diện tích tam giác đều bên trên:
Công thức tính diện tích của một tam giác vuông
- Tam giác vuông là tam giác có một góc bằng 90 độ, góc đó được gọi là góc vuông.
- Công thức:
Ví dụ tam giác ABC vuông tại A. Áp dụng công thức tính diện tích của một tam giác thường để tính, ta có được:
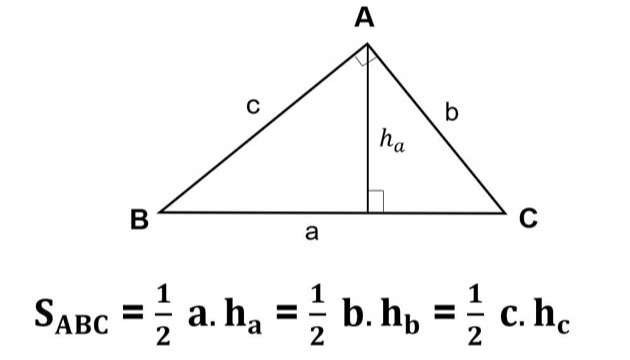
Trong đó:
- A, B, C được gọi là các đỉnh của một tam giác.
- a, b, c lần lượt kí hiệu cho độ dài các cạnh BC, AC, AB của tam giác đó
- ha là đường cao hạ từ đỉnh A tương ứng.
- S là diện tích của hình tam giác.
Tam giác ABC vuông tại B, a, b là độ dài hai cạnh góc vuông BA, BC:
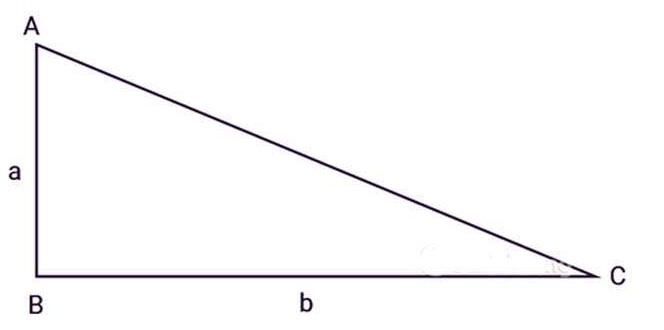
Áp dụng công thức tính diện tích của một tam giác thường cho một tam giác vuông. Chiều cao là 1 trong 2 cạnh góc vuông và cạnh đáy là cạnh còn lại, ta có công thức tính diện tích tam giác vuông như sau:
Ta có ví dụ: Tính diện tích của hình tam giác ABC có độ dài đáy BC là 32cm và chiều cao ha là 22cm.
Tương tự nếu bài toán hỏi ngược về cách tính độ dài, các bạn có thể sử dụng công thức ở trên để suy ngược ra kết quả.
Xem thêm: công thức toán 9 hk1
Công thức tính diện tích của một tam giác vuông cân
- Tam giác vuông cân vừa là một tam giác vuông, nó cũng vừa là tam giác cân.
- Tam giác ABC vuông cân tại A, a là độ dài hai cạnh góc vuông (AB = AC =a):
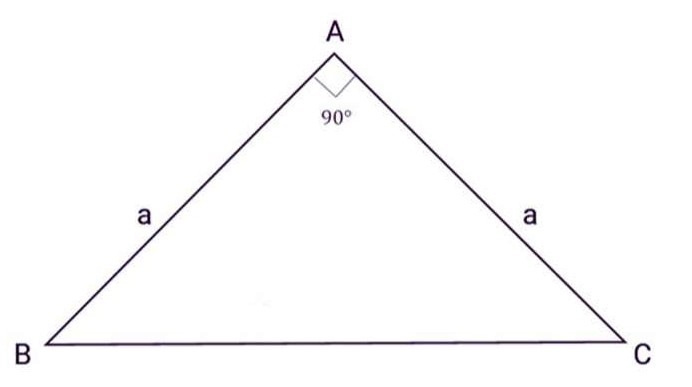
Áp dụng công thức tính diện tích của tam giác vuông cho tam giác vuông cân với chiều cao và cạnh đáy đều bằng nhau, ta được công thức:
Bài viết trên đã tổng hợp đầy đủ các cách tính diện tích hình tam giác và ví dụ minh họa cho từng công thức. Dự báo thời tiết hy vọng rằng, bài viết này sẽ hữu ích đối với quá trình học tập của các bạn trong thời gian sắp tới.
