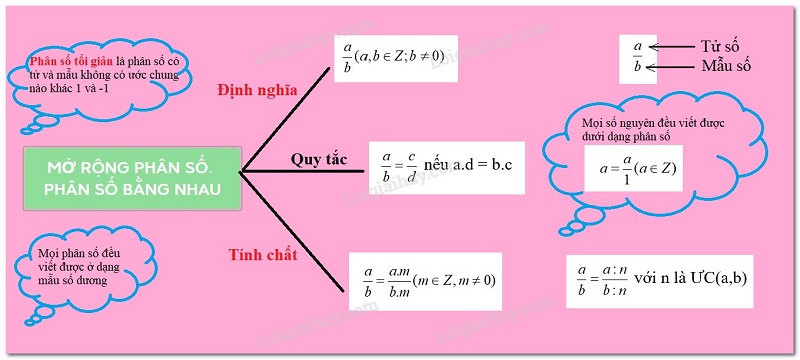
Phân số là gì?
Phân số chính là sự biểu diễn của hai số hữu tỉ, thể hiện dưới dạng tỉ lệ của hai số nguyên. Trong đó, số nguyên phần trên gọi là tử số, số nguyên phần dưới sẽ gọi là mẫu số. Điều kiện bắt buộc mẫu số phải khác 0.
Ký hiệu:
a
-
b
Trong đó, a là tử số, b là mẫu số. (b khác 0)

Ngoài ra, trong toán học thì phân số còn thể hiện cho phép tính chia a : b. Trong đó a sẽ là số chia và b sẽ là số bị chia.
Ví dụ:
⅓ : một phần ba
⅚ ∶ năm phần sáu
¾ : ba phần tư
½ : một phần hai
Tính chất của phân số
Tính chất 1: Nếu nhân cả tử, mẫu số của một phân số này với cùng một số tự nhiên khác số 0 thì ta được một phân số bằng phân số đã cho ban đầu.
Ví dụ:
⅔ = (2*3) / (3*3) = ⅔
Tính chất 2: Nếu chia hết cả tử, mẫu số của một phân số đã cho cùng một số tự nhiên khác số 0 thì ta cũng được một phân số bằng với phân số đã cho.
Ví dụ:
9⁄7 = (9:5) ⁄ (7:5) = 9⁄7
Tính chất 3:
- 1⁄a = a-1
- a ⁄ a = 1 (vì từ và mẫu số bằng nhau)
- a ⁄1 = a một chữ bất kỳ chia cho 1 đều bằng chính nó
Ví dụ:
5⁄5 = 1
4⁄1 = 4 trong đó 4 là tử số và 1 là mẫu số
1⁄2 = 2^-1

Các dạng bài tập về phân số thường gặp
Đối với kiến thức cơ bản về phân số, các em sẽ được làm quen và giải các dạng bài tập sau đây:
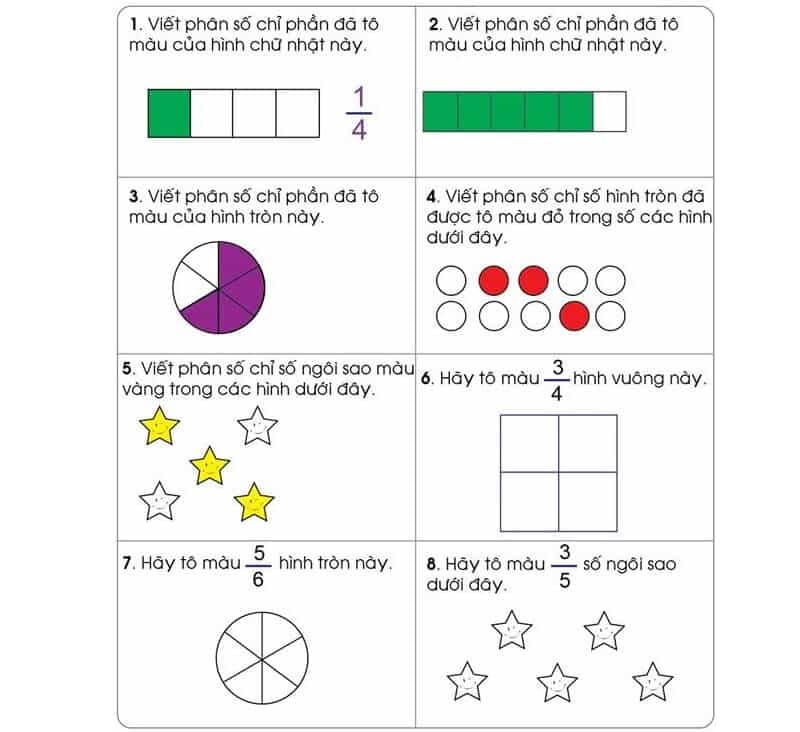
Dạng 1: Rút gọn phân số
Phương pháp giải: Ở một phân số chưa được tối giản, ta có thể rút gọn chúng bằng cách chia cả tử và mẫu số cho ước chung lớn nhất của chúng.
Ví dụ:
70⁄140 = (70:10) ⁄ (140:10) = 7⁄14 = 1⁄2
hoặc 70⁄140 = (70:70) ⁄ (140:70) = ½
Dạng 2: Quy đồng mẫu nhiều phân số
Phương pháp giải: Để quy đồng mẫu số của 2 hoặc nhiều phân số, ta có thể thực hiện theo các bước sau:
- Bước 1: Tìm bội chung nhỏ nhất của các mẫu số để có thể làm thành mẫu số chung (MSC).
- Bước 2: Tìm thừa số phụ cho các mẫu số bằng cách chia MSC cho từng mẫu số.
- Bước 3: Nhân tử số và mẫu số với thừa số phụ tương ứng.
Ví dụ: Quy đồng mẫu số của ⅔ và ¼
Ta có: 3 x 4 = 12, chọn 12 là MSC, ta có:
⅔ = (2 x 4) / (3 x 4) = 8⁄12
¼ = (1 x 3) / (4 x 3) = 3⁄12
Dạng 3: So sánh 2 phân số
Trong dạng bài tập so sánh 2 phần số, ta sẽ chia ra thành nhiều loại khác nhau như sau:
Loại 1: So sánh hai phân số có tử số và mẫu số hoàn toàn khác nhau
- Cho 2 phân số là a ⁄ b, c ⁄ d trong đó b, d khác số 0
- a ⁄ b > c ⁄ d khi và chỉ khi ta có (a * d ) > (b * c)
Ví dụ: So sánh ⅓ và ½
Áp dụng công thức ở trên ta được: 1 * 2 ( = 2) < 1 * 3 (= 3)
Nên suy ra ⅓ < ½
Loại 2: So sánh hai phân số có mẫu số hai phân số bằng nhau
- Trường hợp hai phân số cùng mẫu, ta chỉ cần so sánh 2 tử số với nhau. Nếu tử số của phân số nào lớn hơn thì phân số đó sẽ lớn hơn.
- Nếu 2 phân số cùng mẫu số thì chúng ta chỉ cần so sánh 2 tử số với nhau nếu tử của phân số nào lớn hơn thì phân số đó sẽ lớn hơn.
Cụ thể: a ⁄ b < c ⁄ b khi và chỉ khi a < c
Ví dụ: so sánh 5⁄4 và 7⁄4
Vì 2 phân số trên có cùng mẫu số là 4 nên ta sẽ so sánh 2 tử số: 5 < 7
Nên suy ra 5⁄4 < 7⁄4
Loại 3: Hai phân số có tử số bằng nhau
Trường hợp hai phân số có tử số giống nhau, ta sẽ thực hiện so sánh 2 mẫu số. Nếu mẫu số nào lớn hơn thì phân số đó sẽ được tính là lớn hơn.
Cụ thể: a ⁄ b < c ⁄ d khi và chỉ khi b > c trong đó b, c khác số 0
Ví dụ: cho 2 phân số ⅖ và 2⁄7. Hãy so sánh 2 phân số trên
Vì có cùng tử số và ta có 5 <7 nên 2⁄5> 2⁄7
Dạng 4: Các phép tính toán cơ bản của phân số
Cũng như việc học các dạng toán khác, đối với phân số cũng sẽ có những dạng bài tập về các phép tính cơ bản. Có thể kể đến như:
1. Phép cộng phân số
- Trường hợp 1: Nếu 2 phân số có cùng mẫu số, ta chỉ cần cộng kết quả của 2 tử số với nhau và giữ nguyên mẫu số.
Công thức: a⁄c + b⁄c= (a +b)⁄c
Ví dụ: 5⁄3 + 8⁄3 = (5 +8) ⁄ 3 = 13 ⁄3
- Trường hợp 2: Nếu hai phân số có mẫu số khác nhau, ta phải thực hiện quy đồng mẫu số rồi mới thực hiện phép tính cộng.
Công thức: a ⁄ b + c ⁄ d = (a*d + b*c) ⁄ b*d
Ví dụ: Thực hiện phép tính sau đây: 1⁄4 + 1⁄3 ?
Ta thực hiện quy đồng mẫu số rồi thực hiện phép tính như sau: 1⁄4 + 1⁄3 = 3⁄12 + 4⁄12 = 7⁄12
2. Phép trừ phân số
- Trường hợp 1: Nếu hai phân số có mẫu số giống nhau, ta chỉ cần thực hiện phép trừ hai tử số và giữ nguyên mẫu số.
Công thức : a ⁄ b - c ⁄ b = (a - c) ⁄ b
Ví dụ: 5⁄3 - 4⁄3 = (5 - 4)⁄3 = 1⁄3
- Trường hợp 2: Khi thực hiện phép trừ hai phân số khác mẫu số, ta cần phải quy đồng mẫu rồi mới thực hiện phép tính trừ.
Công thức: a ⁄ b - c ⁄ d = (a*d - b*c) ⁄ (b*d)
Ví dụ: 5⁄2 - 4⁄3 = (5*3 - 4*2) ⁄6 = 7⁄6
3. Phép nhân phân số
Để thực hiện phép tính nhân hai phân số, ta chỉ cần nhân tử số với tử số, mẫu số với mẫu số là được.
Công thức: a ⁄ b * c ⁄ d = ( a*c) ⁄ (b*d)
Ví dụ: 5⁄2 * 4⁄3 = (5*4) ⁄ (2*3) = 20⁄6 = 10⁄3
4. Phép chia phân số
Để chia 2 phân số, ta lấy phân số thứ nhất nhân với đảo ngược của phân số thứ 2.
Công thức: a ⁄ b : c ⁄ d = a ⁄ b * d ⁄ c = (a*d) ⁄ (b*c)
Ví dụ: 5⁄2 : 4⁄3 = 5⁄2 * ¾ = 15⁄8
Bài tập phân số vận dụng
Dưới đây là một số bài tập về phân số để các em cùng nhau luyện tập

Bí quyết học kiến thức phân số hiệu quả
Đối với các bé học tiểu học khi mới làm quen với phần phân số này chỉ mang tính chất cơ bản, nhưng để giúp các bé năm vững chúng, dưới đây là một số bí quyết để bố mẹ tham khảo để hỗ trợ con:
Nắm vững kiến thức cơ bản: Bố mẹ nên hướng dẫn con hiểu thế nào là phân số, các thành phần, các dạng toán, phương pháp giải từng dạng bài tập,… Chỉ khi nắm vững lý thuyết bé mới có thể học thực hành.
Liên hệ phép tính phân số với phép chia: Vốn dĩ phân số là cách thức viết của phép chia. Vậy nên, bố mẹ cần đảm bảo con đã nắm rõ và thực hiện phép tính chia các số tự nhiên chính xác.
Học bảng cửu chương: Phép tính các phân số thường sẽ được dựa vào phép tính nhân và chia. Vậy nên, bảng cửu chương chính là nền tảng để giải được các phép tính này chính xác.
Cùng bé luyện tập thường xuyên: Khi đã nắm rõ được lý thuyết, bố mẹ hãy tạo cơ hội để con được thực hành nhiều hơn từ làm bài tập trong SGK, sách bài tập, tìm hiểu thêm nhiều kiến thức mới trên internet, học qua trò chơi, thực tiễn,… để giúp bé có sự hứng thú và tăng khả năng tiếp thu, ghi nhớ hơn.
Học toán tiểu học cùng Monkey Math: Đây là ứng dụng dạy toán online dành riêng cho đối tượng trẻ mầm non và tiểu học. Với phương pháp dạy học tích cực thông qua video, hình ảnh hoạt họa ngộ nghĩnh, kết hợp cùng hàng ngàn trò chơi tương tác sẽ giúp kích thích tư duy não bộ và năng lực học toán của trẻ tốt hơn.
Kết luận
Trên đây là những kiến thức cơ bản về phân số để các em có thể tìm hiểu và ghi nhớ. Cùng với đó, Monkey có cung cấp thêm một số bí quyết học tập, hy vọng sẽ giúp bố mẹ đưa ra được phương pháp dạy học tốt hơn cho trẻ, giúp con đạt được thành tích học tập tốt nhất.