
Mặt Cầu Là Gì? Công Thức Diện Tích Mặt Cầu, Thể Tích Khối Cầu
1. Mặt cầu là gì? Định nghĩa khối cầu
Trong một không gian, mặt cầu là những điểm cách đều O cố định cho trước một khoảng không đổi R. Tập hợp các điểm trong không gian nằm bên trong mặt cầu và bản thân mặt cầu hợp thành khối cầu hay hình cầu.
Mặt cầu có tâm O và bán kính R chính là tập hợp các điểm trong không gian, cách điểm O một khoảng không đổi cố định r (r>0). Dây cung đi qua tâm O được gọi là đường kính.
Kí hiệu: S (O;R) = {M|OM=R}
Cho mặt cầu S(O;r) cùng điểm A trong không gian:
- OA = r thì điểm A nằm bên trên mặt cầu
- OA < r thì điểm A nằm bên trong mặt cầu.
- OA > r thì điểm A nằm bên ngoài mặt cầu.
Khối cầu hay hình cầu tâm I, bán kính R là tập hợp các điểm thuộc mặt cầu S (I,R) cùng các điểm nằm trong mặt cầu đó.
2. Tính chất
Từ định nghĩa của mặt cầu, ta có tính chất của mặt cầu như sau:
Nếu điểm A ngoài mặt cầu S(O;r) thì ta có:
Độ dài đoạn thẳng nối A với các tiếp điểm sẽ đều bằng nhau.
Qua điểm A sẽ có vô số tiếp tuyến với mặt cầu.
Tập hợp các tiếp điểm là đường tròn nằm bên trên mặt cầu.
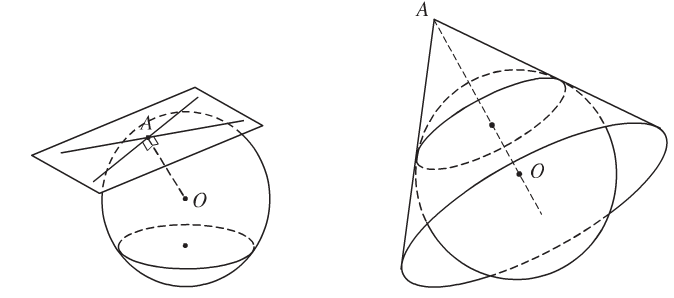
3. Vị trí tương đối mặt cầu với mặt phẳng
Cho mặt cầu S(O,R) và mặt phẳng (P). Ta gọi d =d (O,(P)) .
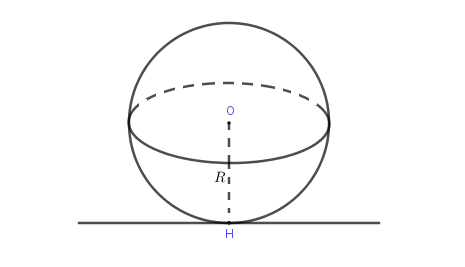
Nếu d = R thì mặt phẳng (P) sẽ tiếp xúc với (S) tại tiếp điểm H. (S) nhận mặt phẳng (P) là tiếp diện.
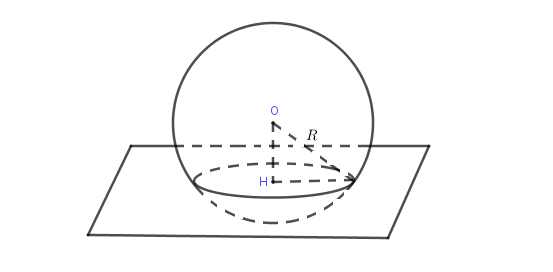
Nếu d < R thì (P) cắt (S) theo giao tuyến là đường tròn nằm bên trên (P), có bán kính $r=\sqrt{R^{2}-d^{2}}$ và tâm H.
d > R thì mặt phẳng (P) và (S) không có điểm chung.
d = 0 thì (P) đi qua tâm O và gọi là mặt phẳng kính, đường tròn giao tuyến có bán kính bằng R gọi là đường tròn lớn.
4. Vị trí tương đối giữa mặt cầu với đường thẳng
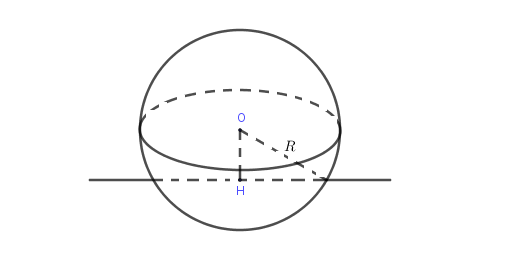
Cho mặt cầu S(O,R) và đường thẳng D. Gọi d = d(O; D).
Nếu d < R thì D cắt (S) tại 2 điểm phân biệt.
d = R thì đường thẳng D tiếp xúc với (S). (D lúc này được gọi là tiếp tuyến của (S)).
Nếu d > R thì D và S không có điểm chung.
5. Tiếp tuyến với mặt cầu
Tiếp tuyến với mặt cầu là:
Ta sẽ không vẽ được tiếp tuyến nào với mặt cầu qua một điểm nằm trong mặt cầu.
Qua một điểm nằm ngoài mặt cầu ta vẽ được vô số tiếp tuyến với mặt cầu. Các tập hợp tiếp điểm với mặt cầu chính là đường tròn nằm bên trên mặt cầu.
Qua một điểm nằm bên trên mặt cầu vẽ được vô số tiếp tuyến với mặt cầu tại điểm đó. Lúc này tập hợp tiếp tuyến chính là mặt phẳng tiếp diện của mặt cầu.
6. Công thức diện tích và thể tích mặt cầu, hình cầu
Mặt cầu khối cầu được tính bằng những công thức dưới đây:
Diện tích mặt cầu:
$S=4.\pi .R^{2}$
Trong đó có R là bán kính mặt cầu.
Thể tích khối cầu:
$V=\frac{4}{3}.\pi .R^{3}$
Trong đó có R là bán kính mặt cầu.
Tham khảo ngay bộ sách ôn thi THPT tổng hợp kiến thức và phương pháp giải mọi dạng bài tập

7. Một số dạng bài tập về mặt cầu và phương pháp giải
7.1. Dạng 1: Xác định tâm và bán kính mặt cầu ngoại tiếp hình lăng trụ đứng
Ta xác định tâm O và O’ của hai đáy.
Tâm của mặt cầu ngoại tiếp lăng trụ lúc này chính là trung điểm của OO’.
$R=IA=\sqrt{OA^{2}+OI^{2}}$ Chú ý: Hình lăng trụ nội tiếp trong một mặt cầu khi nó là hình lăng trụ đứng và có đáy đa giác nội tiếp.
Mặt cầu ngoại tiếp hình hộp chữ nhật ABCD.A’B’C’D’ có:
Tâm là trung điểm AC’
Bán kính R=$\frac{AC'}{2}=\frac{\sqrt{a^{2}+b^{2}+c^{2}}}{2}$
Khi ABCD.A’B’C’D’ là hình lập phương: R=$\frac{a\sqrt{3}}{2}$.
Ví dụ 1: Cho khối cầu ngoại tiếp hình lập phương ABCD.A’B’C’D’ cạnh a. Tính thể tích.
Giải:
Bán kính R mặt cầu ngoại tiếp hình lập phương ABCD.A’B’C’D’ là:
$R=\frac{A'C}{2}=\frac{\sqrt{AA'^{2}+AC^{2}}}{2}=\frac{\sqrt{a^{2}+2a^{2}}}{2}=\frac{a\sqrt{3}}{2}$
Thể tích V=$\frac{4}{3}\pi .R^{3}=\frac{4}{3}\pi .(\frac{a\sqrt{3}}{2})^{3}=\frac{\pi a^{3}\sqrt{3}}{2}$
Ví dụ 2: Tính diện tích S của mặt cầu đi qua 6 đỉnh của hình lăng trụ biết hình lăng trụ tam giác đều ABC.A’B’C’ có các cạnh đều bằng a.
Giải:
Gọi O và O’ lần lượt là tâm của tam giác ABC và A'B'C'.
=> Tâm của mặt cầu ngoại tiếp lăng trụ là trung điểm I của OO’.
=> OI=$\frac{1}{2}OO'=\frac{a}{2}$
Gọi H là trung điểm của BC. Do tam giác ABC đều nên $AH\perp BC$
=> AH=$\frac{a\sqrt{3}}{2}$, OA=$\frac{2}{3}$AH=$\frac{a\sqrt{3}}{3}$
Bán kính mặt cầu ngoại tiếp lăng trụ là:
R=$AI=\sqrt{OI^{2}+OA^{2}}=\sqrt{(\frac{a}{2})^{2}+(\frac{a\sqrt{3}}{3})^{2}}=\frac{a\sqrt{21}}{6}$
Vậy diện tích mặt cầu là:
S=$4\pi R^{2}=4\pi .\frac{21a^{2}}{36}=\frac{7\pi a^{2}}{3}$
7.2. Dạng 2: Mặt cầu ngoại tiếp hình chóp
Để xác định tâm của mặt cầu ngoại tiếp hình chóp, chúng ta thực hiện theo các bước sau:
- Tìm tâm O của mặt đáy.
+ Trong tam giác đều: Giao điểm của 3 đường trung tuyến.
+ Hình vuông và hình chữ nhật: Giao điểm 2 đường chéo.
+ Tam giác vuông: Trung điểm của cạnh huyền.
- Dựng một trục d là đường thẳng đi qua O và vuông góc với đáy ( d song song với chiều cao hình chóp).
- Ta sẽ xác định mặt phẳng trung trực (P) của một cạnh bên.
- Giao điểm của mặt phẳng (P) và d là tâm của mặt cầu ngoại tiếp.
Ví dụ 1: Cho hình chóp S.ABC có SA$\perp $(ABC), AB=1, AC = 2 và $\widehat{BAC}=60^{\circ}$. Gọi M, N là hình chiếu của A trên SB, SC. Tìm bán kính R mặt cầu khi đi qua các điểm A, B, C, M, N.
Giải:
Gọi K là trung điểm của AC => AK = AB = KC = 1
$\widehat{BAC}=60^{\circ}=> \widehat{ABK}=60^{\circ}, \widehat{KBC}=30^{\circ}$ $=>\widehat{ABC}=90^{\circ} (1)$
Theo giả thiết có ANC=$90^{\circ}$ (2)
Ta có:
$\left\{\begin{matrix}BC\perp SA\\ BC\perp AB\end{matrix}\right.$ $=> BC\perp (SAB)$
=> $(SBC)\perp (SAB)$
$AM\perp SB=>AM\perp (SBC)=>AM\perp MC $ (3)
Từ (1), (2), (3) ta có thể suy ra các điểm A, B, C, M, N nội tiếp đường tròn tâm K, bán kính KA=KB=KC=KM=KN=$\frac{1}{2}$AC
Ví dụ 2: Cho hình chóp S.ABCD có cạnh bên SA = 3 và SA$\perp $(ABCD), có đáy ABCD là hình vuông cạnh $2\sqrt{2}$. Mặt phẳng ($\alpha $) đi qua A và vuông góc với SC, cắt cạnh SB, SC, SD lần lượt tại điểm M, N, P. Tính thể tích V của khối cầu ngoại tiếp tứ diện CMNP.
Giải:
Ta có:
$\left\{\begin{matrix}SC\perp AM\\ AM\perp SB\end{matrix}\right.=>AM\perp MC$ $=> \widehat{AMC}=90^{\circ}$
Có $ \widehat{ANC}=90^{\circ}$
Tâm mặt cầu ngoại tiếp tứ diện là trung điểm của AC.C.MNP
=> R=$\frac{AC}{2}=2=>V=\frac{4}{3}\pi R^{3}=\frac{32}{3}\pi $
7.3. Dạng 3: Một số bài toán khác về mặt cầu
Ví dụ 1:Tính diện tích mặt cầu ngoại tiếp lăng trụ biết lăng trụ tam giác đều ABC.A’B’C’ có cạnh đáy là a, góc giữa AB’ với mặt đáy là $45^{\circ}$
Giải:
B’B = AB.tan $45^{\circ}$=a
Gọi O, O’ là trọng tâm tam giác đều ABC và A’B’C’
Trung điểm I của OO’ là tâm mặt cầu ngoại tiếp khối lăng trụ.
Do A’B’C’ là tam giác đều nên O’C’ = $\frac{a\sqrt{3}}{2}$
$IO'=\frac{1}{2}BB'=\frac{a}{2}$
=> R=IC’=$\sqrt{IO'^{2}+O'C'^{2}}=\sqrt{(\frac{a}{2})^{2}+(\frac{a\sqrt{3}}{3})^{2}}=\frac{a\sqrt{21}}{6}$
Vậy diện tích mặt cầu là S=$4\pi R^{2}=\frac{7}{3}\pi a^{2}$
Ví dụ 2: Hãy xác định tâm và bán kính mặt cầu ngoại tiếp tứ diện OABC biết OA=a, OB=b, OC=c và OA, OB, OC đôi một vuông góc với nhau.
Giải
Gọi H là trung điểm AB
Có thể thấy H là tâm đường tròn ngoại tiếp tam giác SAB.
Mp trung trực của SC cắt trục đường tròn (SAB) tại điểm O.
Ta lại có O là tâm mặt cầu ngoại tiếp tứ diện SABC.
Do OHSM là hình chữ nhật nên MS = OH = $\frac{1}{2}c$
R=SO=$\sqrt{SH^{2}+HO^{2}}=\sqrt{\frac{AB^{2}}{4}+HO^{2}} =\sqrt{\frac{SA^{2}+SB^{2}}{4}+HO^{2}}$
Bài viết trên đây là tổng hợp toàn bộ lý thuyết của bài toán về mặt cầu, khối cầu thường gặp trong chương trình toán 12 và phục vụ cho quá trình ôn thi Toán THPT Quốc gia. Để đạt được kết quả cao như mong muốn, các em học sinh hãy ôn luyện thêm thật nhiều công thức toán hình 12 và các dạng bài tập khác nhau. Các bạn có thể truy cập Vuihoc.vn và đăng ký tài khoản để luyện các dạng đề trong kỳ thi THPT Quốc Gia sắp tới.
Bài viết tham khảo thêm:
Hệ tọa độ trong không gian
Link nội dung: https://brightschool.edu.vn/mat-cau-la-gi-cong-thuc-dien-tich-mat-cau-the-tich-khoi-cau-a22403.html