Lý thuyết Đường tròn ngoại tiếp tam giác, đường tròn nội tiếp tam giác Toán 9 Cùng khám phá</>

1. Đường tròn ngoại tiếp tam giác

Định nghĩa đường tròn ngoại tiếp tam giác

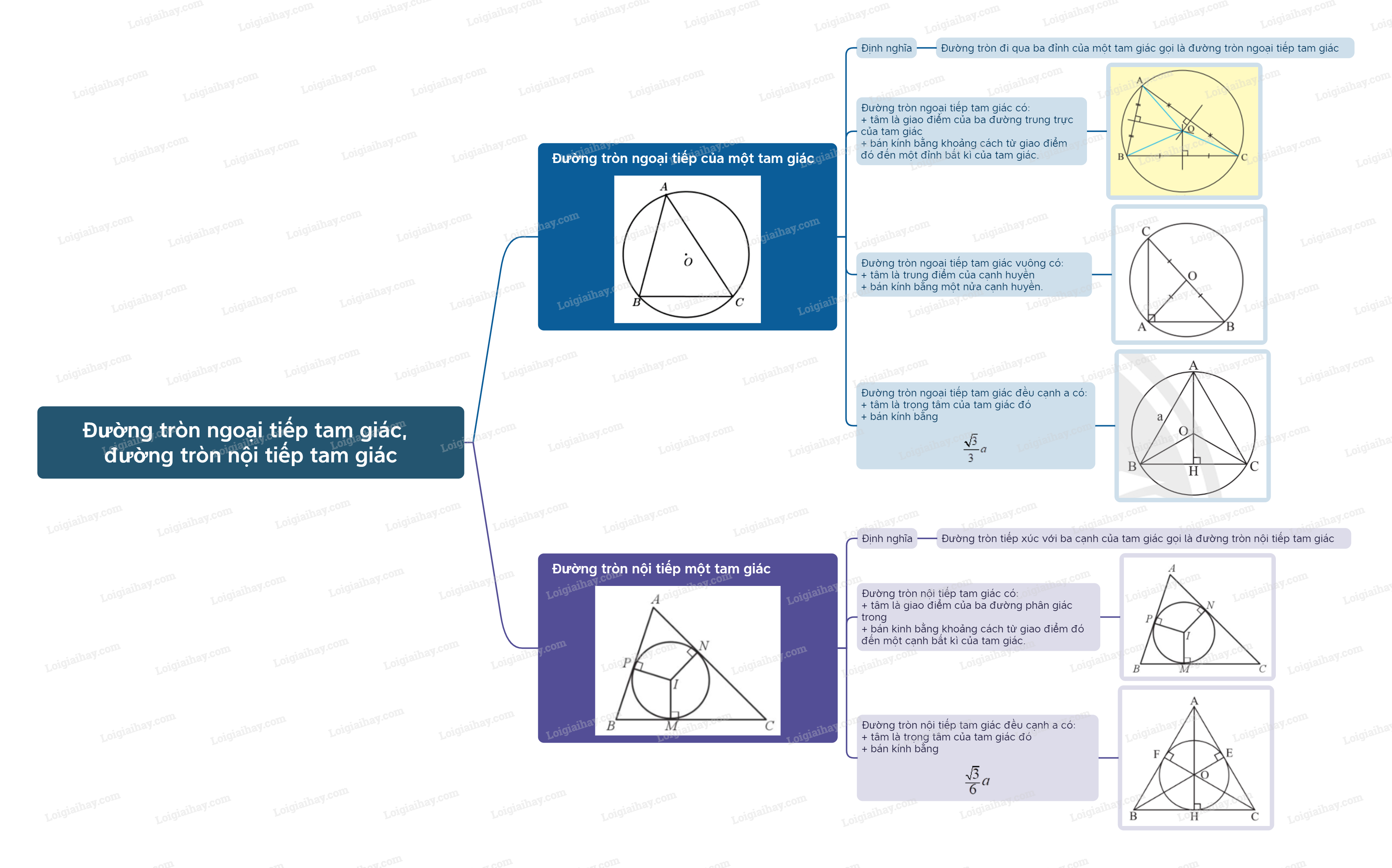
- Đường tròn đi qua ba đỉnh của một tam giác gọi là đường tròn ngoại tiếp tam giác, khi đó tam giác được gọi là tam giác nội tiếp đường tròn.

- Tâm của đường tròn ngoại tiếp tam giác là giao điểm của ba đường trung trực của tam giác đó. Bán kính của đường tròn ngoại tiếp tam giác là khoảng cách từ giao điểm này đến một đỉnh bất kì của tam giác.

Ví dụ:

- Đường tròn (O) ngoại tiếp tam giác ABC. Tam giác ABC nội tiếp đường tròn (O).

- Tâm O là giao điểm của ba đường trung trực của tam giác ABC.

Đường tròn ngoại tiếp tam giác vuông

Đường tròn ngoại tiếp tam giác vuông có tâm là trung điểm của cạnh huyền và bán kính bằng một nửa cạnh huyền.

Ví dụ:

Tam giác ABC nội tiếp đường tròn (O; BO).

Đường tròn ngoại tiếp tam giác đều

Đường tròn ngoại tiếp tam giác đều cạnh a có tâm là trọng tâm của tam giác đó và bán kính bằng \(\frac{{\sqrt 3 }}{3}a\).

Ví dụ:

Đường tròn (O) ngoại tiếp tam giác đều ABC, bán kính \(OA = OB = OC = \frac{{\sqrt 3 }}{3}AB\).

2. Đường tròn nội tiếp một tam giác

Định nghĩa đường tròn nội tiếp tam giác

- Đường tròn tiếp xúc với ba cạnh của tam giác gọi là đường tròn nội tiếp tam giác, khi đó tam giác được gọi là tam giác ngoại tiếp đường tròn.

- Đường tròn nội tiếp tam giác có tâm là giao điểm của ba đường phân giác trong và bán kính bằng khoảng cách từ giao điểm đó đến một cạnh bất kì của tam giác.

Ví dụ:

- Đường tròn (I) nội tiếp tam giác ABC. Tam giác ABC ngoại tiếp đường tròn (I).

- Tâm I là giao điểm của ba đường phân giác của tam giác.

Đường tròn nội tiếp tam giác đều

Đường tròn nội tiếp tam giác đều cạnh a có tâm là trọng tâm của tam giác đó và bán kính bằng \(\frac{{\sqrt 3 }}{6}a\).

Ví dụ:

Đường tròn (O) nội tiếp tam giác đều ABC, bán kính \(OD = OE = \frac{{\sqrt 3 }}{6}AB\).