
Bát diện đều: Khái niệm & cách tính diện tích, thể tích khối bát diện đều
Trong chương trình học của toán bậc trung học phổ thông thì ta có thể gặp được đa dạng về các loại hình từ dễ cho đến phức tạp, điển hình như bát diện đều. Vậy bát diện đều là hình gì? Hình bát diện đều có bao nhiêu cạnh? Bát diện đều có mấy đỉnh? Bát diện đều có bao nhiêu mặt phẳng đối xứng? Chúng ta phải cần biết về những khái niệm, tính chất và công thức của bát diện đều để có thể kiếm điểm từ loại hình này. Chủ đề này sẽ giúp chúng ta giải đáp những thắc mắc đó.
1. Nhắc lại về khối đa diện
Đầu tiên, chúng ta sẽ hệ thống và tóm tắt sơ lược đa diện đều cùng với các kiến thức liên quan đến bát diện đều.
1.1. Khối đa diện
Khối đa diện = hình đa diện + phần không gian được giới hạn bởi hình đa diện.
Ví dụ: Khối tứ diện, khối chóp, khối lăng trụ, khối chóp cụt, khối hộp, khối lập phương,...
Khối đa diện được chia làm hai loại: Khối đa diện lồi và khối đa diện không lồi.
1.2. Khối đa diện đều
Khối đa diện đều là một khối đa diện lồi có hai tính chất sau đây:
• Các mặt là những đa giác đều n cạnh.
• Mỗi đỉnh là đỉnh chung của đúng p cạnh. Khối đa diện đều như vậy gọi là khối đa diện đều loại {n;p}.
» Xem thêm: Những kiến thức cơ bản về khối đa diện và đa diện đều
2. Bát diện đều là hình gì?
a. Khái niệm của hình bát diện đều sẽ bắt nguồn từ định nghĩa của khối đa diện đều, cụ thể như sau:
- Khối đa diện đều là một khối đa diện có tất cả các mặt là các đa giác đều bằng nhau và các cạnh bằng nhau. Và đa diện đều được chia thành đa diện đều lồi và đa diện đều lõm
- Hình bát diện đều là một trong những hình thuộc thành phần của khối đa diện đều. Ngoài bát diện đều thì còn có những khối đa diện đều khác như là: hình tứ diện đều, hình lập phương, hình mười hai mặt đều, hình hai mươi mặt đều.
- Hình bát diện đều là hình đa diện đều loại {3;4}. Có nghĩa là một mặt là tam giác đều. Mỗi đỉnh là đỉnh chung của đúng 4 mặt.
b. Số lượng cạnh, mặt, đỉnh, mặt phẳng đối xứng của hình bát diện, cụ thể như sau:
• Hình bát diện đều có 12 cạnh
• Hình bát diện đều có 6 đỉnh, được hình thành bởi những đỉnh của hình đa giác.
• Hình bát diện đều có 8 mặt, mỗi mặt được tạo nên bởi các mặt, cạnh, đỉnh của hình đa giác.
• Hình bát diện đều có 9 mặt phẳng đối xứng, tương ứng với hai mặt hình đa giác đối diện nhau.
3. Tính chất bát diện đều
Hình bát diện đều có các tính chất như sau:
• Hình bát diện đều thuộc khối đa diện {3;4}
• Mỗi đỉnh của bát diện đều là đỉnh chung của 4 cạnh
• Mỗi mặt là một tam giác đều
• Mỗi đỉnh là đỉnh chung của đúng 4 mặt
4. Cách tính diện tích bát diện đều
∗ Công thức tính diện tích một mặt của hình bát diện đều
∗ Diện tích tất cả các mặt của khối bát diện đều cạnh a là
5. Công thức tính thể tích khối bát diện đều cạnh a
∗ Thể tích khối bát diện đều cạnh a là
6. Bán kính mặt cầu ngoại tiếp bát diện đều
∗ Bán kính mặt cầu ngoại tiếp của bát diện đều là
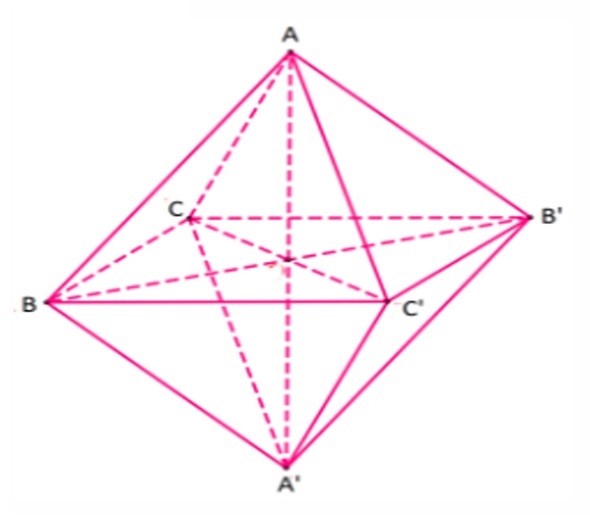
∗ Trục đối xứng là điểm nối giữa hai đỉnh A và A' và đối xứng qua tâm.
7. Bài tập về bát diện đều
Bài 1: Thể tích khối bát diện đều cạnh a là:
A.
B.
C.
D.
ĐÁP ÁN∗ Phương pháp
Chia khối tám mặt đều thành hai khối chóp tứ diện đều.
Tính thể tích khối chóp tứ diện đều bởi công thức: V = h.Sđ
∗ Cách giải
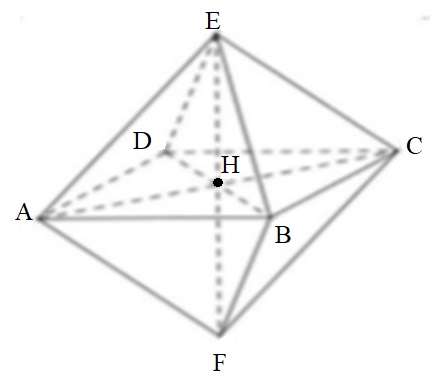
Chia khối tam mặt đều cạnh a thành hai khối chóp tứ diện đều cạnh a.
Khi đó ta có EH là chiều cao của khối chóp EABCD.
Ta có: VEABCDF = 2VEABCD
Gọi h là chiều cao của khối chóp ta được:
⇒
⇒
→ Chọn câu C.
Bài 2: Hình bát diện đều có tất cả bao nhiêu mặt phẳng đối xứng ?
A. 5
B. 6
C. 8
D. 9
ĐÁP ÁN∗ Phương pháp
Vẽ hình, xác định mặt phẳng đối xứng của hình bát diện đều
∗ Cách giải
Hình bát diện đều có tất cả 9 mặt phẳng đối xứng
→ Chọn câu D.
Bài 3: Khối bát diện đều là một khối đa diện lồi loại:
A. {5;3}.
B. {4;3}.
C. {3;4}.
D. {3;5}.
ĐÁP ÁN∗ Phương pháp
Khối đa diện đều mà mỗi mặt là đa giác n cạnh và mỗi đỉnh là đỉnh chung của p cạnh được gọi là khối đa diện đều loại {n; p}.
∗ Cách giải
Khối bát diện đều là khối đa diện đều thuộc loại {3;4}.
→ Chọn câu C.
Bài 4: Số cạnh của khối bát diện đều là:
A. 9
B. 10
C. 11
D. 12
ĐÁP ÁN∗ Phương pháp
Dựa và lý thuyết về khối đa diện đều.
∗ Cách giải
Khối bát diện đều có tất cả 12 cạnh. (Chú ý: có thể coi bát diện đều là gộp của hai khối chóp tứ giác đều có chung đáy)
→ Chọn câu D.
Bài 5: Số đỉnh của khối bát diện đều là
A. 6
B. 7
C. 8
D. 9
ĐÁP ÁN∗ Phương pháp
Dựa vào lý thuyết về khối đa diện.
∗ Cách giải
Khối bát diện đều có tất cả 6 đỉnh
→ Chọn câu A.
Bài 6: Hình bát diện đều có bao nhiêu cạnh?
A. 10
B. 6
C. 8
D. 12
ĐÁP ÁN∗ Phương pháp
∗ Cách giải
Hình bát diện đều có tất cả 12 cạnh.
→ Chọn câu D.
Bài 7: Diện tích các mặt của hình bát diện đều cạnh là 10:
A. 200
B.
C. 100
D.
ĐÁP ÁN∗ Phương pháp
Diện tích các mặt của khối bát diện đều cạnh a là
∗ Cách giải
Diện tích các mặt của hình bát diện đều cạnh là 10 là
→ Chọn câu D.
Trên đây là nội dung bát diện đều về định nghĩa, tính chất, số mặt, số đỉnh, số cạnh, mặt phẳng đối xứng và các công thức tính của hình bát diện đều. Tất cả các dạng toán có liên quan đến khối bát diện đều đa phần thuộc dạng câu hỏi ở mức nhận biết thông hiểu. Vậy qua các kiến thức cùng với bài tập chúng ta đã học thì việc làm tốt các dạng bài về bát diện đều sẽ không quá khó nếu chúng ta nắm bắt rõ những kiến thức cơ bản cùng với công thức khi chúng ta vào cuộc thi THPTQG.
Chịu trách nhiệm nội dung: GV Nguyễn Thị Trang
Link nội dung: https://brightschool.edu.vn/bat-dien-deu-khai-niem-cach-tinh-dien-tich-the-tich-khoi-bat-dien-deu-a22719.html