
Hash Table Data Structure
What is Hash Table?
A Hash table is defined as a data structure used to insert, look up, and remove key-value pairs quickly. It operates on the hashing concept, where each key is translated by a hash function into a distinct index in an array. The index functions as a storage location for the matching value. In simple words, it maps the keys with the value.
What is Load factor?
A hash table’s load factor is determined by how many elements are kept there in relation to how big the table is. The table may be cluttered and have longer search times and collisions if the load factor is high. An ideal load factor can be maintained with the use of a good hash function and proper table resizing.
What is a Hash function?
A Function that translates keys to array indices is known as a hash function. The keys should be evenly distributed across the array via a decent hash function to reduce collisions and ensure quick lookup speeds.
- Integer universe assumption: The keys are assumed to be integers within a certain range according to the integer universe assumption. This enables the use of basic hashing operations like division or multiplication hashing.
- Hashing by division: This straightforward hashing technique uses the key’s remaining value after dividing it by the array’s size as the index. When an array size is a prime number and the keys are evenly spaced out, it performs well.
- Hashing by multiplication: This straightforward hashing operation multiplies the key by a constant between 0 and 1 before taking the fractional portion of the outcome. After that, the index is determined by multiplying the fractional component by the array’s size. Also, it functions effectively when the keys are scattered equally.
Choosing a hash function:
Selecting a decent hash function is based on the properties of the keys and the intended functionality of the hash table. Using a function that evenly distributes the keys and reduces collisions is crucial.
Criteria based on which a hash function is chosen:
- To ensure that the number of collisions is kept to a minimum, a good hash function should distribute the keys throughout the hash table in a uniform manner. This implies that for all pairings of keys, the likelihood of two keys hashing to the same position in the table should be rather constant.
- To enable speedy hashing and key retrieval, the hash function should be computationally efficient.
- It ought to be challenging to deduce the key from its hash value. As a result, attempts to guess the key using the hash value are less likely to succeed.
- A hash function should be flexible enough to adjust as the data being hashed changes. For instance, the hash function needs to continue to perform properly if the keys being hashed change in size or format.
Collision resolution techniques:
Collisions happen when two or more keys point to the same array index. Chaining, open addressing, and double hashing are a few techniques for resolving collisions.
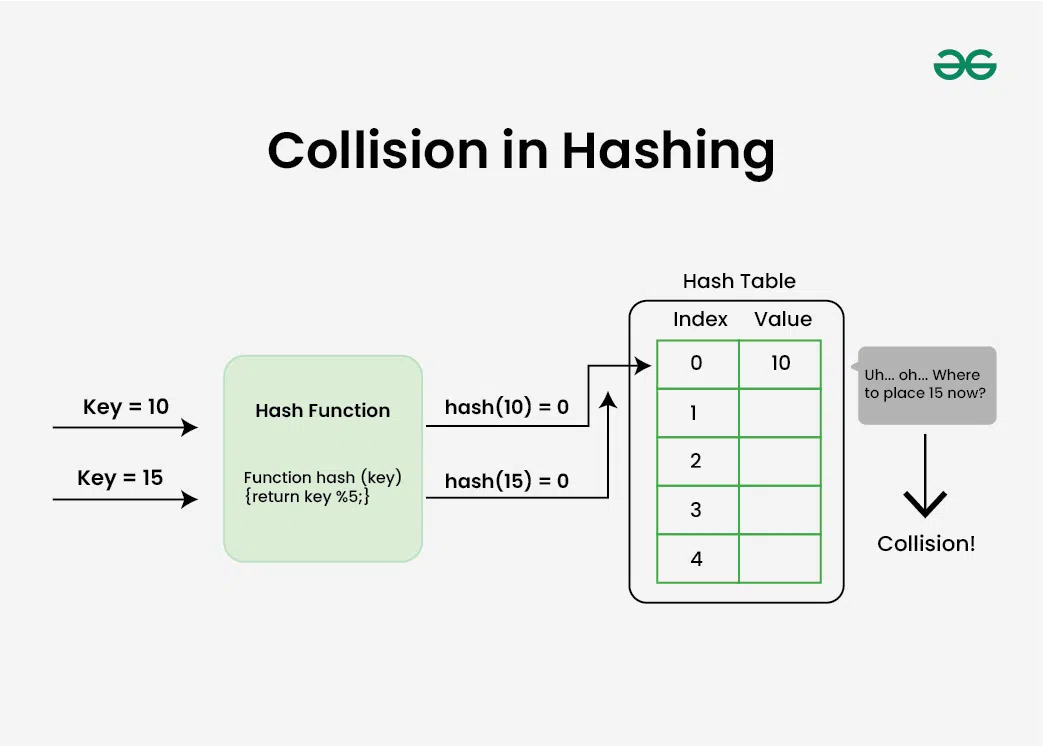
- Open addressing: collisions are handled by looking for the following empty space in the table. If the first slot is already taken, the hash function is applied to the subsequent slots until one is left empty. There are various ways to use this approach, including double hashing, linear probing, and quadratic probing.
- Separate Chaining: In separate chaining, a linked list of objects that hash to each slot in the hash table is present. Two keys are included in the linked list if they hash to the same slot. This method is rather simple to use and can manage several collisions.
- Robin Hood hashing: To reduce the length of the chain, collisions in Robin Hood hashing are addressed by switching off keys. The algorithm compares the distance between the slot and the occupied slot of the two keys if a new key hashes to an already-occupied slot. The existing key gets swapped out with the new one if it is closer to its ideal slot. This brings the existing key closer to its ideal slot. This method has a tendency to cut down on collisions and average chain length.
Dynamic resizing:
This feature enables the hash table to expand or contract in response to changes in the number of elements contained in the table. This promotes a load factor that is ideal and quick lookup times.
Example Implementation of Hash Table
Python, Java, C++, and Ruby are just a few of the programming languages that support hash tables. They can be used as a customized data structure in addition to frequently being included in the standard library.
Example: hashIndex = key % noOfBucketsInsert: Move to the bucket corresponding to the above-calculated hash index and insert the new node at the end of the list.Delete: To delete a node from hash table, calculate the hash index for the key, move to the bucket corresponding to the calculated hash index, and search the list in the current bucket to find and remove the node with the given key (if found).
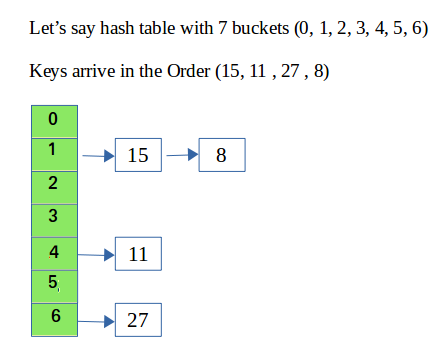
Please refer Hashing | Set 2 (Separate Chaining)for details.
C++ #include using namespace std; struct Hash { int BUCKET; // No. of buckets // Vector of vectors to store the chains vector<vector<int>> table; // Inserts a key into hash table void insertItem(int key) { int index = hashFunction(key); table[index].push_back(key); } // Deletes a key from hash table void deleteItem(int key); // Hash function to map values to key int hashFunction(int x) { return (x % BUCKET); } void displayHash(); // Constructor to initialize bucket count and table Hash(int b) { this->BUCKET = b; table.resize(BUCKET); } }; // Function to delete a key from the hash table void Hash::deleteItem(int key) { int index = hashFunction(key); // Find and remove the key from the table[index] vector auto it = find(table[index].begin(), table[index].end(), key); if (it != table[index].end()) { table[index].erase(it); // Erase the key if found } } // Function to display the hash table void Hash::displayHash() { for (int i = 0; i < BUCKET; i++) { cout << i; for (int x : table[i]) { cout << " -> " << x; } cout << endl; } } // Driver program int main() { // Vector that contains keys to be mapped vector<int> a = {15, 11, 27, 8, 12}; // Insert the keys into the hash table Hash h(7); // 7 is the number of buckets for (int key : a) h.insertItem(key); // Delete 12 from the hash table h.deleteItem(12); // Display the hash table h.displayHash(); return 0; } Java import java.util.ArrayList; public class Hash { // Number of buckets private final int bucket; // Hash table of size bucket private final ArrayList<Integer>[] table; public Hash(int bucket) { this.bucket = bucket; this.table = new ArrayList[bucket]; for (int i = 0; i < bucket; i++) { table[i] = new ArrayList<>(); } } // hash function to map values to key public int hashFunction(int key) { return (key % bucket); } public void insertItem(int key) { // get the hash index of key int index = hashFunction(key); // insert key into hash table at that index table[index].add(key); } public void deleteItem(int key) { // get the hash index of key int index = hashFunction(key); // Check if key is in hash table if (!table[index].contains(key)) { return; } // delete the key from hash table table[index].remove(Integer.valueOf(key)); } // function to display hash table public void displayHash() { for (int i = 0; i < bucket; i++) { System.out.print(i); for (int x : table[i]) { System.out.print(" -> " + x); } System.out.println(); } } // Drive Program public static void main(String[] args) { // array that contains keys to be mapped int[] a = { 15, 11, 27, 8, 12 }; // Create a empty has of BUCKET_SIZE Hash h = new Hash(7); // insert the keys into the hash table for (int x : a) { h.insertItem(x); } // delete 12 from the hash table h.deleteItem(12); // Display the hash table h.displayHash(); } } Python # Python3 program to implement hashing with chaining BUCKET_SIZE = 7 class Hash(object): def __init__(self, bucket): # Number of buckets self.__bucket = bucket # Hash table of size bucket self.__table = [[] for _ in range(bucket)] # hash function to map values to key def hashFunction(self, key): return (key % self.__bucket) def insertItem(self, key): # get the hash index of key index = self.hashFunction(key) self.__table[index].append(key) def deleteItem(self, key): # get the hash index of key index = self.hashFunction(key) # Check the key in the hash table if key not in self.__table[index]: return # delete the key from hash table self.__table[index].remove(key) # function to display hash table def displayHash(self): for i in range(self.__bucket): print("[%d]" % i, end='') for x in self.__table[i]: print(" -> %d" % x, end='') print() # Drive Program if __name__ == "__main__": # array that contains keys to be mapped a = [15, 11, 27, 8, 12] # Create a empty has of BUCKET_SIZE h = Hash(BUCKET_SIZE) # insert the keys into the hash table for x in a: h.insertItem(x) # delete 12 from the hash table h.deleteItem(x) # Display the hash table h.displayHash() C# using System; using System.Collections.Generic; class Hash { int BUCKET; // No. of buckets // List of integers to store values List<int>[] table; public Hash(int V) { this.BUCKET = V; table = new List<int>[BUCKET]; for (int i = 0; i < BUCKET; i++) table[i] = new List<int>(); } // Hash function to map values to key int hashFunction(int x) { return (x % BUCKET); } // Inserts a key into the hash table public void insertItem(int key) { int index = hashFunction(key); table[index].Add(key); } // Deletes a key from the hash table public void deleteItem(int key) { int index = hashFunction(key); table[index].Remove(key); } // Displays the hash table public void displayHash() { for (int i = 0; i < BUCKET; i++) { Console.Write(i + " -> "); foreach (int x in table[i]) Console.Write(x + " "); Console.WriteLine(); } } } class Program { static void Main(string[] args) { // Array that contains keys to be mapped int[] a = { 15, 11, 27, 8, 12 }; int n = a.Length; // Insert the keys into the hash table Hash h = new Hash(7); // 7 is the count of buckets in the hash table for (int i = 0; i < n; i++) h.insertItem(a[i]); // Delete 12 from the hash table h.deleteItem(12); // Display the hash table h.displayHash(); } } JavaScript class Hash { constructor(V) { this.BUCKET = V; // No. of buckets this.table = new Array(V); // Pointer to an array containing buckets for (let i = 0; i < V; i++) { this.table[i] = new Array(); } } // inserts a key into hash table insertItem(x) { const index = this.hashFunction(x); this.table[index].push(x); } // deletes a key from hash table deleteItem(key) { // get the hash index of key const index = this.hashFunction(key); // find the key in (index)th list const i = this.table[index].indexOf(key); // if key is found in hash table, remove it if (i !== -1) { this.table[index].splice(i, 1); } } // hash function to map values to key hashFunction(x) { return x % this.BUCKET; } // function to display hash table displayHash() { for (let i = 0; i < this.BUCKET; i++) { let str = `${i}`; for (let j = 0; j < this.table[i].length; j++) { str += ` -> ${this.table[i][j]}`; } console.log(str); } } } // Driver program const a = [15, 11, 27, 8, 12]; const n = a.length; // insert the keys into the hash table const h = new Hash(7); // 7 is count of buckets in hash table for (let i = 0; i < n; i++) { h.insertItem(a[i]); } // delete 12 from hash table h.deleteItem(12); // display the Hash table h.displayHash();Complexity Analysis of a Hash Table:
For lookup, insertion, and deletion operations, hash tables have an average-case time complexity of O(1). Yet, these operations may, in the worst case, require O(n) time, where n is the number of elements in the table.
Applications of Hash Table:
- Hash tables are frequently used for indexing and searching massive volumes of data. A search engine might use a hash table to store the web pages that it has indexed.
- Data is usually cached in memory via hash tables, enabling rapid access to frequently used information.
- Hash functions are frequently used in cryptography to create digital signatures, validate data, and guarantee data integrity.
- Hash tables can be used for implementing database indexes, enabling fast access to data based on key values.
Link nội dung: https://brightschool.edu.vn/hash-table-data-structure-a24934.html